题目内容
已知集合 ,B={x|log4(x+a)<1},若x∈A是x∈B必要不充分条件,则实数a 的取值范围是________.
,B={x|log4(x+a)<1},若x∈A是x∈B必要不充分条件,则实数a 的取值范围是________.
(-∞,-3]∪[6,+∞)
分析:解指数不等式求得集合A,解一元二次不等式求得集合B,由题意可得B?A,经检验 B≠∅,从而得到-a<4-a≤-2,或 3≤-a<4-a,由此求得实数a 的取值范围.
解答:∵ ={x|x2-x-6>0}={x|x<-2或 x>3}.
={x|x2-x-6>0}={x|x<-2或 x>3}.
B={x|log4(x+a)<1}={x|0<x+a<4}=[x|-a<x<4-a }.
x∈A是x∈B必要不充分条件,可得B?A,∴B=∅或 B≠∅.
当 B=∅时,4-a≤-a,a无解.∴B≠∅.
∴-a<4-a≤-2,或 3≤-a<4-a.
解得 a≥6 或 a≤-3,
故答案为 (-∞,-3]∪[6,+∞).
点评:本题主要考查指数不等式、一元二次不等式的解法,集合间的包含关系,体现了分类讨论的数学思想,属于中档题.
分析:解指数不等式求得集合A,解一元二次不等式求得集合B,由题意可得B?A,经检验 B≠∅,从而得到-a<4-a≤-2,或 3≤-a<4-a,由此求得实数a 的取值范围.
解答:∵
 ={x|x2-x-6>0}={x|x<-2或 x>3}.
={x|x2-x-6>0}={x|x<-2或 x>3}.B={x|log4(x+a)<1}={x|0<x+a<4}=[x|-a<x<4-a }.
x∈A是x∈B必要不充分条件,可得B?A,∴B=∅或 B≠∅.
当 B=∅时,4-a≤-a,a无解.∴B≠∅.
∴-a<4-a≤-2,或 3≤-a<4-a.
解得 a≥6 或 a≤-3,
故答案为 (-∞,-3]∪[6,+∞).
点评:本题主要考查指数不等式、一元二次不等式的解法,集合间的包含关系,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
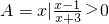 ,B={x|(x+3)(x-a2)≤0}.
,B={x|(x+3)(x-a2)≤0}.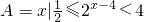 ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|(x+a)(x-2a)≤0},其中a>0.
,B={x|(x+a)(x-2a)≤0},其中a>0. ,B={x|m+1≤x≤3m-1}.
,B={x|m+1≤x≤3m-1}.