题目内容
已知数列{an}满足: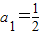 ,
,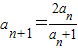 (n∈N*).
(n∈N*).(1)求a2,a3的值;
(2)证明:不等式0<an<an+1对于任意的n∈N*都成立.
【答案】分析:(1)利用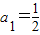 ,
,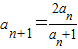 ,将n=1,2代入计算,即可求a2,a3的值;
,将n=1,2代入计算,即可求a2,a3的值;
(2)对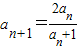 两边取倒数,可得{
两边取倒数,可得{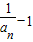 }是以1为首项,
}是以1为首项, 为公比的等比数列,即可确定数列的通项,从而可证结论.
为公比的等比数列,即可确定数列的通项,从而可证结论.
解答:(1)解:∵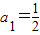 ,
,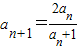
∴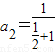 =
= ,
,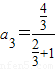 =
=
(2)证明:因为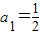 ,
,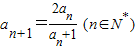 ,所以
,所以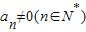 .
.
于是在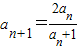 两边取倒数得
两边取倒数得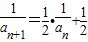 ,
,
整理得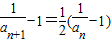 ,而
,而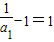 ,
,
所以{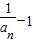 }是以1为首项,
}是以1为首项, 为公比的等比数列,
为公比的等比数列,
所以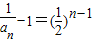 ,所以
,所以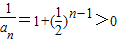 ,
,
所以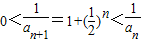 ,
,
故不等式0<an<an+1对于任意n∈N*都成立.
点评:本题考查数列的通项,考查不等式的证明,两边取倒数,证明数列是等比数列是关键.
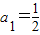 ,
,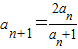 ,将n=1,2代入计算,即可求a2,a3的值;
,将n=1,2代入计算,即可求a2,a3的值;(2)对
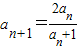 两边取倒数,可得{
两边取倒数,可得{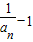 }是以1为首项,
}是以1为首项, 为公比的等比数列,即可确定数列的通项,从而可证结论.
为公比的等比数列,即可确定数列的通项,从而可证结论.解答:(1)解:∵
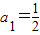 ,
,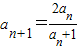
∴
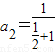 =
= ,
,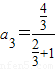 =
=
(2)证明:因为
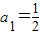 ,
,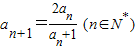 ,所以
,所以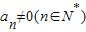 .
.于是在
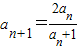 两边取倒数得
两边取倒数得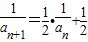 ,
,整理得
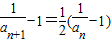 ,而
,而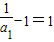 ,
,所以{
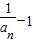 }是以1为首项,
}是以1为首项, 为公比的等比数列,
为公比的等比数列,所以
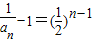 ,所以
,所以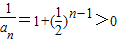 ,
,所以
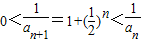 ,
,故不等式0<an<an+1对于任意n∈N*都成立.
点评:本题考查数列的通项,考查不等式的证明,两边取倒数,证明数列是等比数列是关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目