题目内容
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
(1)X的分布列为
2
(2)应该选择种植品种乙
| X | 0 | 1 | 2 | 3 | 4 |
| P |  |  |  |  |  |
(2)应该选择种植品种乙
解:(1)X可能的取值为0,1,2,3,4,
且P(X=0)=
 =
= ,P(X=1)=
,P(X=1)= =
= ,
,P(X=2)=
 =
= ,P(X=3)=
,P(X=3)= =
= ,
,P(X=4)=
 =
= .即X的分布列为
.即X的分布列为| X | 0 | 1 | 2 | 3 | 4 |
| P |  |  |  |  |  |
E(X)=0×
 +1×
+1× +2×
+2× +3×
+3× +4×
+4× =2.
=2.(2)品种甲的每公顷产量的样本平均数和样本方差分别为:
 甲=
甲= (403+397+390+404+388+400+412+406)=400,
(403+397+390+404+388+400+412+406)=400,S2甲=
 (32+(-3)2+(-10)2+42+(-12)2+02+122+62)=57.25.
(32+(-3)2+(-10)2+42+(-12)2+02+122+62)=57.25.品种乙的每公顷产量的样本平均数和样本方差分别为:
 乙=
乙= (419+403+412+418+408+423+400+413)=412,
(419+403+412+418+408+423+400+413)=412,S2乙=
 (72+(-9)2+02+62+(-4)2+112+(-12)2+12)=56.
(72+(-9)2+02+62+(-4)2+112+(-12)2+12)=56.由以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,且两品种的样本方差差异不大,故应该选择种植品种乙.

练习册系列答案
相关题目
 型血的人数占总人口数的比为
型血的人数占总人口数的比为 ,现从中随机抽取3人.
,现从中随机抽取3人. 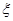 ,求
,求
 的分布列和数学期望.
的分布列和数学期望. 元,正确回答问题B可获奖金
元,正确回答问题B可获奖金 元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大. 表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积.
表示游客在甲、乙、丙三处旅游景点中选择游玩的景点数和没有选择游玩的景点数的乘积. 是R上的偶函数”为事件A,求事件A的概率;
是R上的偶函数”为事件A,求事件A的概率; 的概率分布列及数学期望.
的概率分布列及数学期望. 的概率分布律如下表所示:
的概率分布律如下表所示:







 ,则
,则