Question

已知数列{a_n}的前n项和为S_n=-n²+n，试求出数列{|a_n|}的前n项和T_n．

Answer 1

a₁=S₁=-+=101．

    当n≥2时，a_n=S_n-S_n-1=-3n+104．

    ∵a₁也适合a_n=-3n+104，

    ∴数列{a_n}的通项公式为a_n=-3n+104（n∈N^*）．

    由a_n=-3n+104≥0，得n≤34.7，即当n≤34时，a_n>0；当n≥35时，a_n＜0．

    （1）当n≤34时，

    T_n=|a₁|+|a₂|+…+|a_n|=a₁+a₂+…+a_n=S_n=-n²+n．

    （2）当n≥35时，

    T_n=|a₁|+|a₂|+…+|a₃₄|+|a₃₅|+|a₃₆|+…+|a_n|

    =（a₁+a₂+…+a₃₄）-（a₃₅+a₃₆+…+a_n）

    =2（a₁+a₂+…+a₃₄）-（a₁+a₂+…+a_n）

    =2S₃₄-S_n

    =2（-×34²+×34）-（-n²+n）

    =n²-n+3 502．

    故T_n=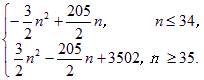

解析:

    对于带绝对值号的数列求和问题，应先弄清n取什么值时a_n>0或a_n<0，然后求解．本题的易错点在于对n在什么范围内取值时a_n>0或a_n<0的讨论．应注意的是当n≥35时，|a_n|=-a_n也是一个等差数列，在这种情况下如何求和的问题要掌握好．由S_n=-n²+n，知S_n是关于n的常数项为0的二次式，所以{a_n}是等差数列，进而求出通项a_n，然后再判断哪些项为正的，哪些项为负的，最后求?出T_n．