题目内容
如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,PA=AC=a,PB=PD=(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角θ的大小;
(3)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
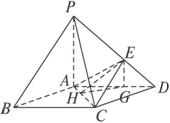
(1)证明:因为底面ABCD是菱形,∠ABC=60°,

所以AB=AD=AC=a.
在△PAB中,
由PA2+AB2=
同理,PA⊥AD,所以PA⊥平面ABCD.
(2)解:作EG∥PA交AD于G,
由PA⊥平面ABCD.知EG⊥平面ABCD.
作GH⊥AC于H,连结EH,则EH⊥AC,∠EHG即为二面角θ的平面角.
又PE∶ED=2∶1,所以EG=1![]() ,AG=
,AG=![]() ,GH=AGsin60°=
,GH=AGsin60°=![]() .
.
从而tanθ=![]() ,θ=30°.
,θ=30°.
(3)解:当F是棱PC的中点时,BF∥平面AEC,证明如下:
因为![]()
![]() ,所以
,所以![]() 、
、![]() 、
、![]() 共面.
共面.
又BF![]() 平面AEC,从而BF∥平面AEC.
平面AEC,从而BF∥平面AEC.

练习册系列答案
相关题目
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD= 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD= 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.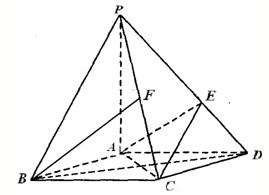 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2