题目内容
已知中心在原点的椭圆的一个焦点为(0, ),且过点
),且过点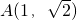 ,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C.
,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C.
(1)求椭圆的标准方程;
(2)求证:直线BC的斜率为定值,并求这个定值.
(3)求三角形ABC的面积最大值.
解:(1)由题意可知c= ,由椭圆的定义求出a=2,所以b=
,由椭圆的定义求出a=2,所以b= ,所以椭圆的方程为:
,所以椭圆的方程为:
(2)由题意得设AB的斜率为k,则AC的斜率为-k
所以 代入得
代入得 ,
,
又∵x1=1∴
同理 ,
, 为定值
为定值
(3)设BC方程为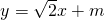

得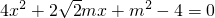
得 A到BC的距离为
A到BC的距离为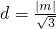
所以
当m2=8-m2时,即m2=4时“=”成立,此时△>0成立.
分析:(1)由题意得c= ,再由由椭圆的定义求出a=2,b=
,再由由椭圆的定义求出a=2,b= ,从而得到椭圆的方程.
,从而得到椭圆的方程.
(2)设AB的斜率为k,则AC的斜率为-k,写出AB的方程与椭圆联立求出B,C坐标得到SC的斜率化简即可
证明直线BC的斜率为定值.
(3)利用弦长公式求出BC 的长,利用得到直线的距离公式求出A到BC的距离,即可求三角形ABC的面积最大值.
点评:本题是中档题,考查椭圆方程的求法,直线与椭圆的位置关系,三角形面积求法,最大值的求法,考查计算能力,转化思想.
 ,由椭圆的定义求出a=2,所以b=
,由椭圆的定义求出a=2,所以b= ,所以椭圆的方程为:
,所以椭圆的方程为:
(2)由题意得设AB的斜率为k,则AC的斜率为-k
所以
 代入得
代入得 ,
,又∵x1=1∴

同理
 ,
, 为定值
为定值(3)设BC方程为
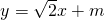

得
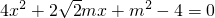
得
 A到BC的距离为
A到BC的距离为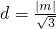
所以

当m2=8-m2时,即m2=4时“=”成立,此时△>0成立.
分析:(1)由题意得c=
 ,再由由椭圆的定义求出a=2,b=
,再由由椭圆的定义求出a=2,b= ,从而得到椭圆的方程.
,从而得到椭圆的方程.(2)设AB的斜率为k,则AC的斜率为-k,写出AB的方程与椭圆联立求出B,C坐标得到SC的斜率化简即可
证明直线BC的斜率为定值.
(3)利用弦长公式求出BC 的长,利用得到直线的距离公式求出A到BC的距离,即可求三角形ABC的面积最大值.
点评:本题是中档题,考查椭圆方程的求法,直线与椭圆的位置关系,三角形面积求法,最大值的求法,考查计算能力,转化思想.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
已知中心在原点的椭圆C的右焦点为F(
,0),直线y=x与椭圆的一个交点的横坐标为2,则椭圆方程为( )
| 15 |
A、
| ||||
B、x2+
| ||||
C、
| ||||
D、
|