题目内容
已知双曲线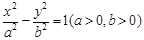 的两焦点为
的两焦点为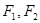 ,过
,过 作
作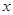 轴的垂线交双曲线于
轴的垂线交双曲线于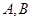 两点,若
两点,若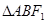 内切圆的半径为
内切圆的半径为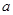 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
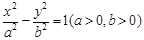 的两焦点为
的两焦点为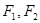 ,过
,过 作
作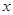 轴的垂线交双曲线于
轴的垂线交双曲线于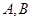 两点,若
两点,若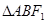 内切圆的半径为
内切圆的半径为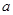 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )A.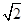 | B.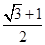 | C.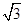 | D.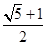 |
D
试题分析:由双曲线的定义得:
 ,两式相加得:
,两式相加得: 又在双曲线中,
又在双曲线中, ,所以
,所以 的周长为:
的周长为: ∵
∵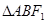 内切圆的半径为
内切圆的半径为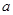 ,∴
,∴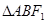 面积为:
面积为: ,又
,又 ,∴
,∴ ,
,整理得:
 ,所以双曲线的离心率为
,所以双曲线的离心率为
点评在解题过程中要注意隐含条件的挖掘,注意应用三角形面积的不同计算方法建立关于
 的等式求离心率.
的等式求离心率.
练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
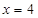 ,右焦点
,右焦点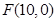 ,离心率
,离心率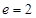 ,求双曲线方程.
,求双曲线方程. 方程为
方程为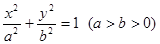 ,左、右焦点分别是
,左、右焦点分别是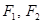 ,若椭圆
,若椭圆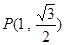 到
到 .
. 是椭圆
是椭圆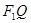 中点
中点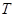 的轨迹方程;
的轨迹方程;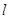 过定点
过定点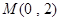 ,且与椭圆
,且与椭圆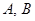 ,若
,若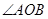 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线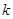 的取值范围.
的取值范围. 是以
是以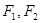 为左、右焦点的双曲线
为左、右焦点的双曲线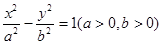 左支上一点,且满足
左支上一点,且满足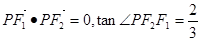 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )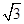
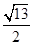
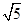
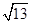
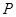 是椭圆
是椭圆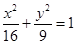 上的点,
上的点, 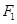 、
、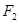 是椭圆的两个焦点,则
是椭圆的两个焦点,则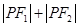 的值为
的值为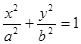 的左焦点作直线交椭圆于
的左焦点作直线交椭圆于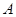 、
、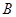 两点,若存在直线使坐标原点
两点,若存在直线使坐标原点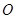 恰好在以
恰好在以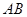 为直径的圆上,则椭圆的离心率取值范围是
为直径的圆上,则椭圆的离心率取值范围是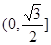
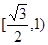
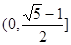
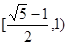
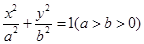 中,
中,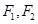 分别是其左右焦点,若
分别是其左右焦点,若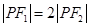 ,则该椭圆离心率的取值范围是 ( )
,则该椭圆离心率的取值范围是 ( )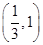
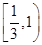
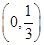
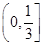
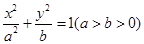 的左、右焦点分别为
的左、右焦点分别为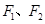 ,离心率
,离心率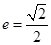 ,
, 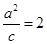 .
.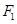 的直线
的直线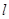 与该椭圆交于
与该椭圆交于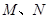 两点,且
两点,且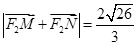 ,求直线
,求直线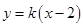
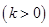 与抛物线
与抛物线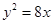 相交于
相交于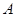 、
、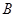 两点,
两点,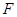 为抛物线的焦点,若
为抛物线的焦点,若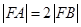 ,则
,则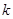 的值为 。
的值为 。