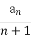题目内容
已知向量a=(sin(α+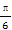
),1),b=(4,4cosα-
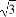),若a⊥b,则sin(α+
)=( )
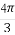(A)-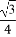
(B)-
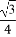(C) (D)
B
【解析】∵a⊥b,∴a·b=4sin(α+
)+4cosα-
=0,
即sin(α+)+cosα=
,
即sinαcos+cosαsin+cosα=,
即
sinα+
cosα=,
故
sinα+cosα=
,故sin(α+
)=,
又sin(α+
)=-sin(α+)=-.
故选B.
练习册系列答案
阅读快车系列答案
相关题目
