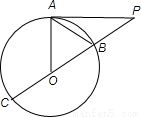
题目内容
过圆O上任意一点A作圆O的切线AP，（O为圆心）AP=| 3 |
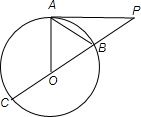
分析：本题求弦AB的长，由于弦AB在三角形中，故可以研究三角形AOB的边角关系以确定AB长度的求法．由题设条件不难得出圆的半径为1，而三角形AOB是一个等边三角形，故可求得弦AB的长．
解答：解：由题设条件∠OAP=90°
又连接PO并延长交圆O于B、C两点，且B、O是PC的三等分点，
∴B是OP的中点，故可得△AOB是正三角形，∠AOP=
又AP=
，tan
=
=
=
，
故OA=1，所以AB=1
故答案为1．
又连接PO并延长交圆O于B、C两点，且B、O是PC的三等分点，
∴B是OP的中点，故可得△AOB是正三角形，∠AOP=
| π |
| 3 |
又AP=
| 3 |
| π |
| 3 |
| AP |
| OA |
| ||
| OA |
| 3 |
故OA=1，所以AB=1
故答案为1．
点评：本题考点是与圆有关的比例线段，本题考查在三角形中求线段的长度，线段的长度一般用勾股定理，切割线定理等建立方程求解，本题由于条件的特殊性，采取了以角来确定三角形是等边三角形，再根据三等分点的性质来求线段的长度，对条件的组合方式较巧妙．
练习册系列答案
全能测控一本好卷系列答案
相关题目
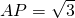；连接PO并延长交圆O于B、C两点，且B、O是PC的三等分点，则弦AB的长为 ________．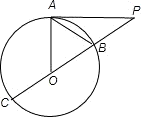
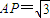；连接PO并延长交圆O于B、C两点，且B、O是PC的三等分点，则弦AB的长为 ．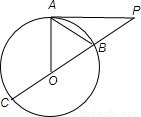
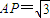；连接PO并延长交圆O于B、C两点，且B、O是PC的三等分点，则弦AB的长为 ．