题目内容
已知函数![]() .
.
![]() (Ⅰ)讨论
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)设点P在曲线![]() 上,若该曲线在点P处的切线
上,若该曲线在点P处的切线![]() 通过坐标原点,求
通过坐标原点,求![]() 的方程
的方程
解析:
(1)![]()
当![]() 和
和![]() 时,
时,![]() ;
;
当![]() 和
和![]() 时,
时,![]()
因此,![]() 在区间
在区间![]() 和
和![]() 是减函数,
是减函数,
![]() 在区间
在区间![]() 和
和![]() 是增函数。
是增函数。
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,由
,由![]() 过原点知,
过原点知,![]() 的方程为
的方程为
![]()
因此 ![]() ,
,
即 ![]()
整理得 ![]()
解得 ![]() 或
或 ![]()
因此切线![]() 的方程为
的方程为 ![]() 或
或 ![]() 。
。

练习册系列答案
相关题目
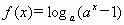 ,(
,(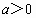 ,
,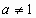 ),
),
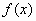 的定义域;
的定义域;
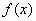 的单调性.
的单调性.