题目内容
(本小题满分12分)
如图,在多面体 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ,
, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.

⑴求证: 平面
平面 ;
;
⑵求二面角 的余弦值.
的余弦值.
如图,在多面体
 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ,
, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.
⑴求证:
 平面
平面 ;
;⑵求二面角
 的余弦值.
的余弦值.证明:⑴∵
 ,
, ,∴
,∴ .
.在四边形
 中,由
中,由 ,
, ,
, ,可证得
,可证得 ,
,又由
 平面
平面 ,得
,得 ,
,∵正方形
 中
中 ,∴
,∴ 平面
平面 ,
,∵
 平面
平面 ,
, ∴
∴ ,
,∵
 ,∴
,∴ 平面
平面 ; …………………………6分
; …………………………6分⑵以
 、
、 、
、 为
为 、
、 、
、 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则
 、
、 、
、 、
、 .
. 、
、 、
、 ,
,分别求得平面
 与平面
与平面 的一个法向量
的一个法向量 ,
, ,
,向量
 与
与 的夹角的余弦值为
的夹角的余弦值为
∴二面角
 的余弦值为
的余弦值为 .
.略

练习册系列答案
相关题目
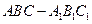 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
,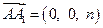 ,其中
,其中 、
、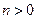

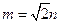 ,求直线
,求直线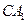 与平面
与平面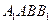 所成角的大小。
所成角的大小。 n作为点P的坐标
n作为点P的坐标 ,求:
,求:
 上的概率;
上的概率; 外的概率.
外的概率.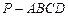 中,底面
中,底面 是平行四边形,
是平行四边形,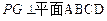 ,垂足为
,垂足为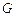 ,
,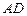 上,且
上,且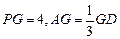 ,
,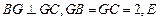 是
是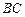 的中点.
的中点.
 与
与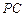 所成的角的余弦值;
所成的角的余弦值;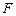 是棱
是棱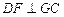 ,求
,求 的值.
的值.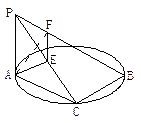
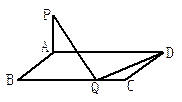
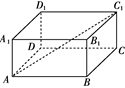 (第20题) (第21题)
(第20题) (第21题)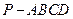 的底面是边长为6 的正方形,侧棱
的底面是边长为6 的正方形,侧棱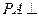 底面
底面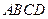 ,且
,且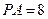 ,则该四棱椎的体积是 ▲ .
,则该四棱椎的体积是 ▲ .  ∥
∥ 且
且 ,则
,则
 的关系是__________.
的关系是__________.