题目内容
设F1,F2分别是椭圆 +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,求点P的横坐标为
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,求点P的横坐标为
- A.1
- B.

- C.2

- D.

D
分析:先根据椭圆方程求得椭圆的半焦距c,根据PF1⊥PF2,推断出点P在以 为半径,以原点为圆心的圆上,进而求得该圆的方程与椭圆的方程联立求得交点的坐标,则根据点P所在的象限确定其横坐标.
为半径,以原点为圆心的圆上,进而求得该圆的方程与椭圆的方程联立求得交点的坐标,则根据点P所在的象限确定其横坐标.
解答:由题意半焦距c=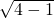 =
= ,
,
又∵PF1⊥PF2,
∴点P在以 为半径,以原点为圆心的圆上,
为半径,以原点为圆心的圆上,
由 ,解得x=±
,解得x=± ,y=±
,y=±
∴P坐标为( ,
, ).
).
故选D.
点评:本题主要考查了椭圆的简单性质,椭圆与圆的位置关系.考查了考生对椭圆基础知识的综合运用.属基础题.
分析:先根据椭圆方程求得椭圆的半焦距c,根据PF1⊥PF2,推断出点P在以
 为半径,以原点为圆心的圆上,进而求得该圆的方程与椭圆的方程联立求得交点的坐标,则根据点P所在的象限确定其横坐标.
为半径,以原点为圆心的圆上,进而求得该圆的方程与椭圆的方程联立求得交点的坐标,则根据点P所在的象限确定其横坐标.解答:由题意半焦距c=
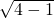 =
= ,
,又∵PF1⊥PF2,
∴点P在以
 为半径,以原点为圆心的圆上,
为半径,以原点为圆心的圆上,由
 ,解得x=±
,解得x=± ,y=±
,y=±
∴P坐标为(
 ,
, ).
).故选D.
点评:本题主要考查了椭圆的简单性质,椭圆与圆的位置关系.考查了考生对椭圆基础知识的综合运用.属基础题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
设F1、F2分别是椭圆
+
=1(a>b>0)的左、右焦点,P是其右准线上纵坐标为
c(c为半焦距)的点,且|F1F2|=|F2P|,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 设F1、F2分别是椭圆
设F1、F2分别是椭圆