题目内容
二次函数y=f（x）的图象是开口向上的抛物线，对称轴是x=3，则下列式子中错误的是（ ）
分析：根据二次函数的图象和对称轴，分别判断即可．
解答：解：∵二次函数y=f（x）的图象是开口向上的抛物线，对称轴是x=3，
∴当x≤3时，函数f（x）单调递减，
当x≥3时，函数f（x）单调递增．
∴f（2）=f（4），
又f（4）＞f（
），
∴f（2）＞f（
），
即B错误．
故选：B．
∴当x≤3时，函数f（x）单调递减，
当x≥3时，函数f（x）单调递增．
∴f（2）=f（4），
又f（4）＞f（
| 15 |
∴f（2）＞f（
| 15 |
即B错误．
故选：B．
点评：本题主要考查二次函数的图象和性质，利用二次函数的对称性和单调性是解决本题的关键，比较基础．
练习册系列答案
相关题目
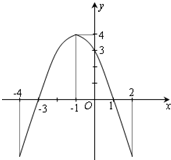如图是一个二次函数y=f（x）的图象．
已知二次函数y=f（x）的图象如图所示．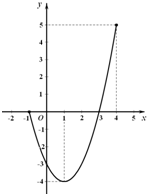
二次函数y=f（x）的图象的一部分如图所示．