题目内容
记实数 …
… 中的最大数为
中的最大数为 {
{ …
… },最小数为min{
},最小数为min{ …
… }.已知
}.已知 的三边边长为
的三边边长为 、
、 、
、 (
( ),定义它的倾斜度为
),定义它的倾斜度为 则“t=1”是“
则“t=1”是“ 为等边三角形”的( )
为等边三角形”的( )
| A.充分布不必要的条件 | B.必要而不充分的条件 |
| C.充要条件 | D.既不充分也不必要的条件 |
B
解析试题分析:因为, 的三边边长为
的三边边长为 、
、 、
、 (
( ),所以,
),所以, ,
, =
= ,
, =
= 或
或 ,
,
所以, t=1时,可能三角形为等腰三角形,反之,
t=1时,可能三角形为等腰三角形,反之, 为等边三角形时,t=1,即“t=1”是“
为等边三角形时,t=1,即“t=1”是“ 为等边三角形”的必要而不充分的条件,选B。
为等边三角形”的必要而不充分的条件,选B。
考点:新定义问题,充要条件的概念。
点评:简单题,关键是理解新定义概念,明确计算方法。涉及充要条件问题,可以利用“定义法、等价关系法、集合关系法”加以判断。

练习册系列答案
相关题目
已知复数 ,则“
,则“ ”是“
”是“ 为纯虚数”的( )
为纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是( )
A.命题“若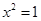 ,则 ,则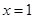 ” 的否命题为“若 ” 的否命题为“若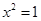 ,则 ,则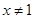 ” ” |
B.“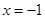 ”是“ ”是“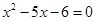 ”的必要而不充分条件 ”的必要而不充分条件 |
C.命题“存在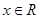 ,使得 ,使得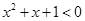 ”的否定是“对任意 ”的否定是“对任意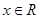 ,均有 ,均有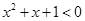 ” ” |
D.命题“若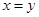 ,则 ,则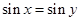 ”的逆否命题为真命题 ”的逆否命题为真命题 |
命题 :
: 是奇数,
是奇数, :
: 是偶数(
是偶数( )则下列说法中正确的是( )
)则下列说法中正确的是( )
A. 或 或 为真 为真 | B. 且 且 为真 为真 | C.非 为真 为真 | D.非 为假 为假 |
若 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
条件 ,条件
,条件 ,则
,则 是
是 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
下列命题中正确的是( )
| A.第一象限角必是锐角 | B.终边相同的角相等 |
| C.负角必是第四象限角 | D.相等的角终边必相同 |
 “是函数
“是函数 在区间
在区间 内单调递增”的( )
内单调递增”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |