题目内容
若函数f（x），g（x）分别是R上的奇函数、偶函数，且满足
，则有
- A.f′（x）+g（x）=0
- B.f′（x）-g（x）=0
- C.f（x）+g′（x）=0
- D.f（x）-g′（x）=0
A
分析：先由已知，及f（-x）=-f（x），g（-x）=g（x），可求出f（x），g（x），再求出f′（x），g′（x），即可判断出答案．
解答：∵函数f（x），g（x）分别是R上的奇函数、偶函数，∴?x∈R，f（-x）=-f（x），g（-x）=g（x），
由x满足，则f（-x）+g（-x）=
，即-f（x）+g（x）=ex，
联立
解之得f（x）=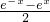
，g（x）=
，
于是
，
，∴f′（x）+g（x）=0．
故选A．
点评：本题综合考查了函数的奇偶性及导数，熟练掌握它们是解决问题的关键．
分析：先由已知
，及f（-x）=-f（x），g（-x）=g（x），可求出f（x），g（x），再求出f′（x），g′（x），即可判断出答案．解答：∵函数f（x），g（x）分别是R上的奇函数、偶函数，∴?x∈R，f（-x）=-f（x），g（-x）=g（x），
由x满足
，则f（-x）+g（-x）=，即-f（x）+g（x）=ex，联立
解之得f（x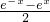）=，g（x）=，于是
，，∴f′（x）+g（x）=0．故选A．
点评：本题综合考查了函数的奇偶性及导数，熟练掌握它们是解决问题的关键．
练习册系列答案
相关题目