题目内容
下列四个命题中,真命题的序号是
①?x∈R,x+
≥2 ②?x∈R,x+
≥2 ③?x∈R,|x+1|≤0 ④?x∈R,|x+1|>0.
②③
②③
.①?x∈R,x+
| 1 |
| x |
| 1 |
| x |
分析:根据全称命题和特称命题的定义进行判断.
解答:解:①当x≤0时,x+
≥2不成立,∴①错误.
②当x=2时,满足 x+
≥2,∴②正确.
③当x=-1时,|x+1|≤0成立,∴③正确.
④当x=-1时,|x+1|=0,∴成立?x∈R|x+1|>0不成立,∴④错误.
故真命题是②③.
故答案为:②③.
| 1 |
| x |
②当x=2时,满足 x+
| 1 |
| x |
③当x=-1时,|x+1|≤0成立,∴③正确.
④当x=-1时,|x+1|=0,∴成立?x∈R|x+1|>0不成立,∴④错误.
故真命题是②③.
故答案为:②③.
点评:本题主要考查含有量词的命题的真假的判断,特称命题主要存在即成立,全称命题只要能举出反例,则全称命题为假.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
(如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是( )
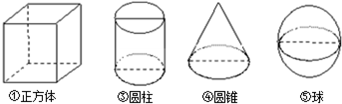

| A、①② | B、②③ | C、②④ | D、③④ |
 (2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )
(2012•厦门模拟)某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录,下列四个结论中,不正确的是( )