题目内容
如图2-4-15,PA、PB是⊙O的两条切线,A、B为切点,C是
上一点,已知⊙O的半径为r,PO =2r,设∠PAC+∠PBC =α,∠APB =β,则α与β的大小关系为( )A.α＞β B.α=β C.α＜β D.不能确定
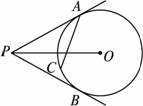
图2-4-15
思路解析:连结AB、AO,∵PA、PB为切线,?
∴∠PAC=∠ABC,∠PBC=∠BAC.?
∴α=∠PAC+∠PBC=∠PAC+∠BAC=∠PAB =∠PBA =
=
.
∵AO =r,PA切⊙O于A,∴AO⊥PA,且PO=2r.?
∴∠APO = 30°.
∴∠APB =2∠APO=60°.∴β=60°.?
∴α=
(180°-60°)=60°.∴α=β.
答案:B
练习册系列答案
名校课堂系列答案
相关题目
为迎接建党90周年，某班开展了一次“党史知识竞赛”，竞赛分初赛和决赛两个阶段进行，在初赛后，把成绩（满分为100分，分数均匀整数）进行统计，制成如图的频率分布表：
（Ⅰ）求a，b，c，d的值；
（Ⅱ）决赛规则如下：为每位参加决赛的选手准备四道题目，选手对其依次作答，答对两道就终止答题，并获得一等奖，若题目答完仍然只答对一道，则获得二等奖．某同学进入决赛，每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同．设该同学决赛中答题个数为X，求X的分布列以及X的数学期望．
| 序号 | 分组（分数段） | 频数（人数） | 频率 |
| 1 | [0，60） | a | 0.1 |
| 2 | [60，75） | 15 | b |
| 3 | [75，90） | 20 | 0.4 |
| 4 | [90，100] | c | d |
| 合计 | 50 | 1 | |
（Ⅱ）决赛规则如下：为每位参加决赛的选手准备四道题目，选手对其依次作答，答对两道就终止答题，并获得一等奖，若题目答完仍然只答对一道，则获得二等奖．某同学进入决赛，每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同．设该同学决赛中答题个数为X，求X的分布列以及X的数学期望．
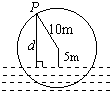如图，一个半径为10米的水轮按逆时针方向每分钟转4圈．记水轮上的点P到水面的距离为d米（P在水面下则d为负数），则d（米）与时间t（秒）之间满足关系式：d=Asin（ωt+φ）+k（A＞0，ω＞0），
如图：过抛物线y2=4x上的点A（1，2）作切线l交x轴与直线x=-4分别于D，B．动点P是抛物线y2=4x上的一点，点E在线段AP上，满足
给出下列5个命题：