题目内容
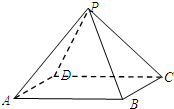 (2007•杨浦区二模)在正四棱锥P-ABCD中(如图),若异面直线PA与BC所成角的正切值为2,底面边长AB=4.
(2007•杨浦区二模)在正四棱锥P-ABCD中(如图),若异面直线PA与BC所成角的正切值为2,底面边长AB=4.(1)求侧棱与底面ABCD所成角的大小.
(2)求四棱锥P-ABCD的体积.
分析:(1)要求侧棱与底面ABCD所成角的大小,关键是找出侧棱在底面ABCD上的射影.过P作斜高,则∠PAD为异面直线PA与BC所成的角,进而可求侧棱与底面ABCD所成角的大小
(2)求四棱锥P-ABCD的体积,关键是求出底面积与高,进而利用公式求解.
(2)求四棱锥P-ABCD的体积,关键是求出底面积与高,进而利用公式求解.
解答:解:(1)过P作斜高PE,PO⊥底面ABCD,AD∥BC∴∠PAD为异面直线PA与BC所成的角θ且tanθ=2(3分)
在Rt△PEA中tanθ=2=
且AE=2所以PE=4,PA=2
(5分)
正四棱锥P-ABCD的高为PO=2
在Rt△POA中,∴sin∠PAO=
∴∠PAO=arcsin
,
侧棱与底面ABCD所成角的大小为arcsin
( 或写成arccos
) (7分)
(2)VP--ABCD=
•42•2
=
(14分)
在Rt△PEA中tanθ=2=
| PE |
| AE |
| 5 |
正四棱锥P-ABCD的高为PO=2
| 3 |
| ||
| 5 |
| ||
| 5 |
侧棱与底面ABCD所成角的大小为arcsin
| ||
| 5 |
| ||
| 5 |
(2)VP--ABCD=
| 1 |
| 3 |
| 3 |
32
| ||
| 3 |
点评:本题的考点是直线与平面所成的角,主要考查侧棱与底面ABCD所成角的大小,关键是找出侧棱在底面ABCD上的射影,考查几何体的体积,属于中档题.

练习册系列答案
相关题目