题目内容
已知函数f(x)=(x-a)2ex,a∈R.(1)求f(x)的单调区间;
(2)对任意的x∈(-∞,1],不等式f(x)≤4e恒成立,求a的取值范围;
(3)求证:当a=2,2<t<6时,关于x的方程
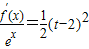 在区间[-2,t]上总有两个不同的解.
在区间[-2,t]上总有两个不同的解.
【答案】分析:(1)f′(x)=2(x-a)ex+(x-a)2ex=(x-a)[x-(a-2)]ex.令f′(x)=0,得x1=a-2,x2=.由此能求出f(x)的单调递区间.
(2)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2.当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1),得-1≤a≤1;当1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2)=4ea-2≤4e3-2=4e;当a>3时,f(1)=(a-1)2e>4e,f(x)≤4e不恒成立.由此能求出a的取值范围.
(III)由f′(x)=x(x-2)ex,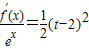 ,知
,知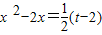 2,令g(x)=
2,令g(x)=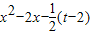 2,
2,
从而问题转化为证明当2<t<6时,函数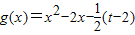 2在[-2,t]与x轴有两个不同的交点,由此能够证明当a=2,2<t<6时,关于x的方程
2在[-2,t]与x轴有两个不同的交点,由此能够证明当a=2,2<t<6时,关于x的方程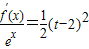 在区间[-2,t]上总有两个不同的解.
在区间[-2,t]上总有两个不同的解.
解答:解:(1)f′(x)=2(x-a)ex+(x-a)2ex,
=(x-a)[x-(a-2)]ex.…2分
令f′(x)=0,得x1=a-2,x2=a.
当x变化时,f′(x)、f(x)的变化如下:
所以f(x)的单调递增区间是(-∞,a-2),(a,+∞),
单调递减区间是(a-2,a).…6分
(2)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2.
①当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1),
由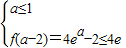 ,f(1)=(a-1)•2e≤4e,解得-1≤a≤1;
,f(1)=(a-1)•2e≤4e,解得-1≤a≤1;
②当a-2≤1<a,即1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2),
此时f(a-2)=4ea-2≤4e3-2=4e;
③当a-2>1,即a>3时,f(1)=(a-1)2e>4e,f(x)≤4e不恒成立.
综上,a的取值范围是[-1,3].…12分
(III)∵f′(x)=x(x-2)ex,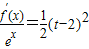 ,
,
∴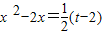 2,
2,
令g(x)=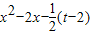 2,
2,
从而问题转化为证明当2<t<6时,
函数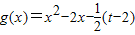 2在[-2,t]与x轴有两个不同的交点,
2在[-2,t]与x轴有两个不同的交点,
∵g(-2)>0,g(t)>0,g(0)<0,
∴g(x)=0在[-2,t]上有解,且有两解.
所以,当a=2,2<t<6时,关于x的方程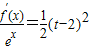 在区间[-2,t]上总有两个不同的解.(15分)
在区间[-2,t]上总有两个不同的解.(15分)
点评:本题考查利用导数求闭区间上函数的最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,仔细解答.
(2)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2.当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1),得-1≤a≤1;当1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2)=4ea-2≤4e3-2=4e;当a>3时,f(1)=(a-1)2e>4e,f(x)≤4e不恒成立.由此能求出a的取值范围.
(III)由f′(x)=x(x-2)ex,
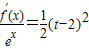 ,知
,知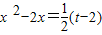 2,令g(x)=
2,令g(x)=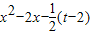 2,
2,从而问题转化为证明当2<t<6时,函数
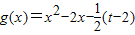 2在[-2,t]与x轴有两个不同的交点,由此能够证明当a=2,2<t<6时,关于x的方程
2在[-2,t]与x轴有两个不同的交点,由此能够证明当a=2,2<t<6时,关于x的方程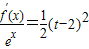 在区间[-2,t]上总有两个不同的解.
在区间[-2,t]上总有两个不同的解.解答:解:(1)f′(x)=2(x-a)ex+(x-a)2ex,
=(x-a)[x-(a-2)]ex.…2分
令f′(x)=0,得x1=a-2,x2=a.
当x变化时,f′(x)、f(x)的变化如下:
| x | (-∞,a-2) | a-2 | (a-2,a) | a | (a,+∞) |
| f′(x) | + | - | + | ||
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
单调递减区间是(a-2,a).…6分
(2)由(Ⅰ)得[f(x)]极大=f(a-2)=4ea-2.
①当a≤1时,f(x)在(-∞,1]上的最大值为f(a-2)或f(1),
由
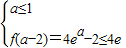 ,f(1)=(a-1)•2e≤4e,解得-1≤a≤1;
,f(1)=(a-1)•2e≤4e,解得-1≤a≤1;②当a-2≤1<a,即1<a≤3时,f(x)在(-∞,1]上的最大值为f(a-2),
此时f(a-2)=4ea-2≤4e3-2=4e;
③当a-2>1,即a>3时,f(1)=(a-1)2e>4e,f(x)≤4e不恒成立.
综上,a的取值范围是[-1,3].…12分
(III)∵f′(x)=x(x-2)ex,
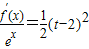 ,
,∴
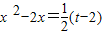 2,
2,令g(x)=
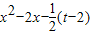 2,
2,从而问题转化为证明当2<t<6时,
函数
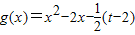 2在[-2,t]与x轴有两个不同的交点,
2在[-2,t]与x轴有两个不同的交点,∵g(-2)>0,g(t)>0,g(0)<0,
∴g(x)=0在[-2,t]上有解,且有两解.
所以,当a=2,2<t<6时,关于x的方程
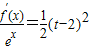 在区间[-2,t]上总有两个不同的解.(15分)
在区间[-2,t]上总有两个不同的解.(15分)点评:本题考查利用导数求闭区间上函数的最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|