Question

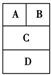
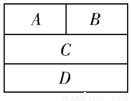
如图，用4种不同的颜色涂入图中的矩形A，B，C，D中，要求相邻的矩形涂色不同，则不同的涂法有

1. A.
   72种
2. B.
   48种
3. C.
   24种
4. D.
   12种

Answer 1

A
试题分析：先涂A的话，有4种选择，若选择了一种，则B有3种，而为了让C与AB都不一样，则C有2种，再涂D的话，只要与C涂不一样的就可以，也就是D有3种，所以一共有4x3x2x3=72种，故选A。
考点：本题主要考查分步计数原理的应用。
点评：从某一区域涂起，按要求“要求相邻的矩形涂色不同”，分步完成。