题目内容
(1)求过点P(-1,2)且与两坐标轴的正半轴所围成的三角形面积等于 的直线方程;
的直线方程;(2)求圆心在y轴上且经过点M(-2,3),N(2,1)的圆的方程.
【答案】分析:(1)设直线方程为 ,由点P(-1,2)在直线上,知2a-b=ab,由
,由点P(-1,2)在直线上,知2a-b=ab,由 ,知ab=1,由此能求出直线方程.
,知ab=1,由此能求出直线方程.
(2)由圆心C在线段MN的中垂线上, ,MN的中点是(0,2),知MN的中垂线方程是y=2x+2,由此能求出圆的方程.
,MN的中点是(0,2),知MN的中垂线方程是y=2x+2,由此能求出圆的方程.
解答:解:(1)由题意设直线方程为 …(1分)
…(1分)
∵点P(-1,2)在直线上,
∴ ,
,
则2a-b=ab…(2分)
又∵ ,
,
则ab=1…(3分)
∴ ,
,
消去b整理得2a2-a-1=0,
解得a=1或 (舍去)…(5分)
(舍去)…(5分)
由ab=1解得b=1,
故所求直线方程是x+y=1…(6分)
(2)由题意圆心C在线段MN的中垂线上…(7分)
∵ ,
,
MN的中点是(0,2)…(8分)
∴MN的中垂线方程是y=2x+2…(9分)
令x=0则y=2,
圆心C(0,2),
半径r= ,…(11分)
,…(11分)
所求圆的方程为x2+(y-2)2=5.…(12分)
点评:本题考查直线方程的求法和圆的方程的求法,是基础题.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 ,由点P(-1,2)在直线上,知2a-b=ab,由
,由点P(-1,2)在直线上,知2a-b=ab,由 ,知ab=1,由此能求出直线方程.
,知ab=1,由此能求出直线方程.(2)由圆心C在线段MN的中垂线上,
 ,MN的中点是(0,2),知MN的中垂线方程是y=2x+2,由此能求出圆的方程.
,MN的中点是(0,2),知MN的中垂线方程是y=2x+2,由此能求出圆的方程.解答:解:(1)由题意设直线方程为
 …(1分)
…(1分)∵点P(-1,2)在直线上,
∴
 ,
,则2a-b=ab…(2分)
又∵
 ,
,则ab=1…(3分)
∴
 ,
,消去b整理得2a2-a-1=0,
解得a=1或
 (舍去)…(5分)
(舍去)…(5分)由ab=1解得b=1,
故所求直线方程是x+y=1…(6分)
(2)由题意圆心C在线段MN的中垂线上…(7分)
∵
 ,
,MN的中点是(0,2)…(8分)
∴MN的中垂线方程是y=2x+2…(9分)
令x=0则y=2,
圆心C(0,2),
半径r=
 ,…(11分)
,…(11分)所求圆的方程为x2+(y-2)2=5.…(12分)
点评:本题考查直线方程的求法和圆的方程的求法,是基础题.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
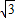 ,求直线l的方程.
,求直线l的方程.