Question

已知函数f(x)=

2x

x2+1

，g(x)=

1

3

ax3-a2x(a≠0)．
（I）当x∈[0，3]时，求f（x）的值域；
（II）对于任意x₁∈[0，3]，总存在x₂∈[0，3]，使f（x₁）=

1

6

g(x2)成立，求实数a的取值范围．

Answer 1

分析：（I）对函数f（x）求导，令导数f′（x）=0，求得函数f（x）的极值，然后和f（0）函数f（3）比较大小，最大的作为其最大值，最小的作为其最小值，从而求得f（x）的值域；
（II）对于任意x₁∈[0，3]，总存在x₂∈[0，3]，使f（x₁）=

1

6

g(x2)成立，转化为函数f（x）的值域是函数g（x）的值域的子集，下面求解函数函数g（x）的值域，求法同（I），列出关于a的不等式组，即可求得实数a的取值范围．

解答：解：（I）f′(x)=

2-2x2

(x2+1)2

=

2(1+x)(1-x)

(x2+1)2

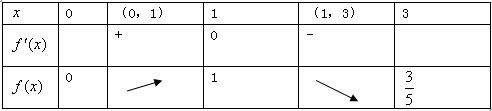
∴函数f（x）的值域为[0，1]．
（II）设x∈[0，3]时，函数y=

1

6

g(x)的值域为A，∵对于任意x₁∈[0，3]，
总存在x₁∈[0，3]，使f（x₀）=

1

6

g(x1)，∴[0，1]⊆A∵g'（x）=ax²-a²=a（x²-a）
（1）当a＜0时，x∈（0，3）时，g'（x）＜0，函数g（x）在（0，3）上单调递减，
∴g（3）≤g（x）≤g（0）∵g（0）=0∴不满足[0，1]⊆A
（2）当a＞0时，g′(x)=a(x-

a

)(x+

a

)，
令g'（x）=0，∴x1=

a

或x2=-

a

（舍去）
①当0＜

a

＜3，即0＜a＜9时，如列表

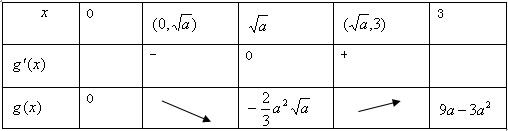
∵g(0)=0，g(

a

)=0，若[0，1]⊆A，
则

1

6

g(3)=

1

6

(9a-3a2)≥1∴1≤a≤2
②当

a

≥3，即a≥9时，x∈（0，3）时，g'（x）＜0，函数g（x）在（0，3）上单调递减
∴g（3）≤g（x）≤g（0）∵g（0）=0，∴不满足[0，1]⊆A
综上，实数a的取值范围是1≤a≤2．

点评：考查应用导数研究函数的最值问题，特别问题（II）转化为求函数的最值问题，体现了转化的思想方法，在求函数g（x）的最值过程中，体现了分类讨论的思想，属难题．