Question

已知集合M={(x,y)|y²=2x},N={(x,y)|(x-a)²+y²=9},求M∩N≠的充要条件.

Answer 1

解：∵M∩N≠的充要条件是方程组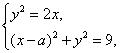至少有一组解.

消去y得（x-a）²+2x=9至少有一个非负实根.

问题转化为方程：x²-2(a+1)x+a²-9=0至少有一个非负实根的充要条件.

Δ=4（a+1）²-4(a²-9)≥0，即2a+10≥0,

∴{a|a≥-5}为全集U.

设方程x²-2(a+1)x+a²-9=0

两根都为负根时满足

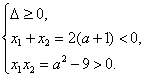即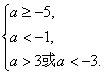

∴-5≤a＜-3.

设集合A={a|-5≤a＜-3}.

原方程至少有一个非负实根的充要条件是a∈A={a|a≥-3},

故M∩N≠的充要条件是a∈{a|a≥-3}.