题目内容
已知函数 的图象与x轴相切于点S(s,0).
的图象与x轴相切于点S(s,0).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数f(x)的图象与过坐标原点O的直线l相切于点T(t,f(t)),且f(t)≠0,证明:1<t<e;(注:e是自然对数的底)
(Ⅲ)在(Ⅱ)的条件下,记直线ST的倾斜角为α,试证明: .
.
(Ⅰ)解:由 ,得
,得 .…(1分)
.…(1分)
∵函数 的图象与x轴相切于点S(s,0),
的图象与x轴相切于点S(s,0),
∴ ,…①且f(s)=
,…①且f(s)= ….②…(2分)
….②…(2分)
联立①②得c=e, .…(3分)
.…(3分)
∴ .…(4分)
.…(4分)
(Ⅱ)证明: .
.
∵函数 的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
∴直线l的方程为: ,
,
又∵T在直线l上,∴实数t必为方程 ….③的解.…(5分)
….③的解.…(5分)
令 ,则
,则 ,
,
解g′(t)>0得 ,g′(t)<0得
,g′(t)<0得 .
.
∴函数y=g(t)在 递减,在
递减,在 递增.…(7分)
递增.…(7分)
∵ ,且函数y=g(t)在
,且函数y=g(t)在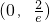 递减,
递减,
∴ 是方程
是方程 在区间
在区间 内的唯一一个解,
内的唯一一个解,
又∵ ,∴
,∴ 不合题意,即
不合题意,即 .…(8分)
.…(8分)
∵g(1)=2-e<0, ,函数y=g(t)在
,函数y=g(t)在 递增,
递增,
∴必有1<t<e.…(9分)
(Ⅲ)证明:∵T(t,f(t)),
∴ ,
,
由③得 ,…(10分)
,…(10分)
∵t>0,且0≤α<π,∴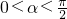 .
.
∵1<t<e,∴ ,…(11分)
,…(11分)
∵ ,
, ,…(13分)
,…(13分)
∴ ,
,
∵y=tanx在 单调递增,∴
单调递增,∴ .…(14分)
.…(14分)
分析:(Ⅰ)求导数,利用函数 的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;
的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;
(Ⅱ)先确定直线l的方程为: ,利用T在直线l上,可得实数t必为方程
,利用T在直线l上,可得实数t必为方程 ,构造函数
,构造函数 ,确定函数的单调性,从而可得
,确定函数的单调性,从而可得 是方程
是方程 在区间
在区间 内的唯一一个解,由此可证结论;
内的唯一一个解,由此可证结论;
(Ⅲ)先证明 ,利用y=tanx在
,利用y=tanx在 单调递增,即可证得结论.
单调递增,即可证得结论.
点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、曲线的切线方程、函数的零点、解不等式、直线方程和三角函数等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、函数与方程思想、特殊与一般思想.
 ,得
,得 .…(1分)
.…(1分)∵函数
 的图象与x轴相切于点S(s,0),
的图象与x轴相切于点S(s,0),∴
 ,…①且f(s)=
,…①且f(s)= ….②…(2分)
….②…(2分)联立①②得c=e,
 .…(3分)
.…(3分)∴
 .…(4分)
.…(4分)(Ⅱ)证明:
 .
.∵函数
 的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,∴直线l的方程为:
 ,
,又∵T在直线l上,∴实数t必为方程
 ….③的解.…(5分)
….③的解.…(5分)令
 ,则
,则 ,
,解g′(t)>0得
 ,g′(t)<0得
,g′(t)<0得 .
.∴函数y=g(t)在
 递减,在
递减,在 递增.…(7分)
递增.…(7分)∵
 ,且函数y=g(t)在
,且函数y=g(t)在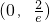 递减,
递减,∴
 是方程
是方程 在区间
在区间 内的唯一一个解,
内的唯一一个解,又∵
 ,∴
,∴ 不合题意,即
不合题意,即 .…(8分)
.…(8分)∵g(1)=2-e<0,
 ,函数y=g(t)在
,函数y=g(t)在 递增,
递增,∴必有1<t<e.…(9分)
(Ⅲ)证明:∵T(t,f(t)),

∴
 ,
,由③得
 ,…(10分)
,…(10分)∵t>0,且0≤α<π,∴
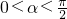 .
.∵1<t<e,∴
 ,…(11分)
,…(11分)∵
 ,
, ,…(13分)
,…(13分)∴
 ,
,∵y=tanx在
 单调递增,∴
单调递增,∴ .…(14分)
.…(14分)分析:(Ⅰ)求导数,利用函数
 的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;
的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;(Ⅱ)先确定直线l的方程为:
 ,利用T在直线l上,可得实数t必为方程
,利用T在直线l上,可得实数t必为方程 ,构造函数
,构造函数 ,确定函数的单调性,从而可得
,确定函数的单调性,从而可得 是方程
是方程 在区间
在区间 内的唯一一个解,由此可证结论;
内的唯一一个解,由此可证结论;(Ⅲ)先证明
 ,利用y=tanx在
,利用y=tanx在 单调递增,即可证得结论.
单调递增,即可证得结论.点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、曲线的切线方程、函数的零点、解不等式、直线方程和三角函数等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、函数与方程思想、特殊与一般思想.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
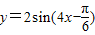
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )


 的图象与x轴交点为
的图象与x轴交点为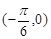 ,相邻最高点坐标为
,相邻最高点坐标为 .
.  的表达式;
的表达式; 的单调增区间;
的单调增区间; 在
在 上的最值.
上的最值. 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 B.
B.
 D.
D.
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 B.
B.
 D.
D.