题目内容
随机询问72名不同性别的大学生在购买食物时是否看营养说明.其中看营养说明的44人中有28人是男生;而不看营养说明的女生有20人,男生仅有8人.
(1)根据以上数据建立一个2×2列联表;
(2)判断能否在犯错误的概率不超过0.005的前提下认为性别与是否看营养说明之间有关系?
附:K2=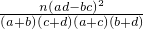 ,其中n=a+b+c+d为样本容量
,其中n=a+b+c+d为样本容量
| P(K2≥K0) | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 5.024 | 6.635 | 7.879 | 10.828 |
解:(1)性别与看营养说明列联表
(2)∵K2的观测值K= ≈8.416,
≈8.416,
而P(K2≥7.879)≈0.005,
∴在犯错误的概率不超过0.005的前提下认为“性别与是否看营养说明之间有关系”.
分析:(1)根据所给的条件中的数据写出性别与看营养说明的列联表,这种表格是一个固定的格式,注意数字不要弄错位置.
(2)根据上一问做出的列联表,把要用的数据代入求观测值的公式,做出观测值,同题目中的临界值进行比较,看出在犯错误的概率不超过0.005的前提下认为“性别与是否看营养说明之间有关系”.
点评:本题考查独立性检验的应用,这种问题解题时关键要看清题意,看出各种情况下的量,注意在数字运算上不要出错.
| 女 | 男 | 总计 | |
| 看营养说明 | 16 | 28 | 44 |
| 不看营养说明 | 20 | 8 | 28 |
| 总计 | 36 | 36 | 72 |
 ≈8.416,
≈8.416,而P(K2≥7.879)≈0.005,
∴在犯错误的概率不超过0.005的前提下认为“性别与是否看营养说明之间有关系”.
分析:(1)根据所给的条件中的数据写出性别与看营养说明的列联表,这种表格是一个固定的格式,注意数字不要弄错位置.
(2)根据上一问做出的列联表,把要用的数据代入求观测值的公式,做出观测值,同题目中的临界值进行比较,看出在犯错误的概率不超过0.005的前提下认为“性别与是否看营养说明之间有关系”.
点评:本题考查独立性检验的应用,这种问题解题时关键要看清题意,看出各种情况下的量,注意在数字运算上不要出错.

练习册系列答案
相关题目
随机询问72名不同性别的大学生在购买食物时是否看营养说明.其中看营养说明的44人中有28人是男生;而不看营养说明的女生有20人,男生仅有8人.
(1)根据以上数据建立一个2×2列联表;
(2)判断能否在犯错误的概率不超过0.005的前提下认为性别与是否看营养说明之间有关系?
附:K2=
,其中n=a+b+c+d为样本容量
(1)根据以上数据建立一个2×2列联表;
(2)判断能否在犯错误的概率不超过0.005的前提下认为性别与是否看营养说明之间有关系?
附:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥K0) | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 5.024 | 6.635 | 7.879 | 10.828 |
通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
性别与读营养说明列联表
| 女 | 男 | 总计 |
读营养说明 | 16 | 28 | 44 |
不读营养说明 | 20 | 8 | 28 |
总计 | 36 | 36 | 72 |
请问性别和读营养说明之间在多大程度上有关系?
通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下2×2列联表:
| 女生 | 男生 | 合计 |
读营养说明 | 16 | 28 | 44 |
不读营养说明 | 20 | 8 | 28 |
合计 | 36 | 36 | 72 |
请问性别和读营养说明之间在多大程度上有关系?
通过随机询问72名不同性别的大学生在购买食物时是否看生产日期,得到如下列联表:
性别与看生产日期列联表
| 女 | 男 | 总 计 |
读生产日期 | 16 | 28 | 44 |
不读生产日期 | 20 | 8 | 28 |
总 计 | 36 | 36 | 72 |
请问性别和读生产日期之间在多大程度上有关系?
