Question

【题目】（本小题满分14分）已知函数．

（Ⅰ）求函数的单调区间；

（Ⅱ）若存在两条直线，都是曲线的切线，求实数的取值范围；

（Ⅲ）若，求实数的取值范围．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）；．（Ⅲ）

【解析】

试题分析：（Ⅰ），对a进行分类讨论：当时，，则函数的单调递减区间是．当时，令，得．的单调递减区间是，单调递增区间是；（Ⅱ）因为 存在两条直线，都是曲线的切线，

所以 至少有两个不等的正实根，令得，记其两个实根分别为．

则 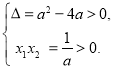解得．再说明当时，曲线在点处的切线分别为，是两条不同的直线即可；（Ⅲ）只需分类讨论．

试题解析：（Ⅰ）． 1分

当时，，则函数的单调递减区间是． 2分

当时，令，得．

当变化时，，的变化情况如下：

	↘	极小值	↗

所以 的单调递减区间是，单调递增区间是． 4分

（Ⅱ）因为 存在两条直线，都是曲线的切线，

所以 至少有两个不等的正实根． 5分

令得，记其两个实根分别为．

则 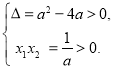解得． 7分

当时，曲线在点处的切线分别为，．

令．

由得（不妨设），且当时，，即在上是单调函数．

所以 ．

所以 ，是曲线的两条不同的切线．

所以 实数的取值范围为． 9分

（Ⅲ）当时，函数是内的减函数．

因为 ，

而，不符合题意． 11分

当时，由（Ⅰ）知：的最小值是．

（ⅰ）若，即时，，

所以，符合题意．

（ⅱ）若，即时，．

所以，符合题意．

（ⅲ）若，即时，有．

因为 ，函数在内是增函数，

所以 当时，．

又因为 函数的定义域为，

所以 ．

所以 符合题意．

综上所述，实数的取值范围为． 14分