题目内容
已知函数f(x)=x3-
x2+8.
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,2]上的最值.
| 3 |
| 2 |
(1)求f(x)的单调区间;
(2)求f(x)在区间[0,2]上的最值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数的运算法则可得f′(x)=3x2-3x=3x(x-1),分别解出f′(x)>0,与f′(x)<0,即可得出单调区间;
(2)令f′(x)=0,解得x1=0,x2=1,把x在(0,2)上变化时,f′(x),f(x)的变化情况列出表格即可得出.
(2)令f′(x)=0,解得x1=0,x2=1,把x在(0,2)上变化时,f′(x),f(x)的变化情况列出表格即可得出.
解答:
解:(1)f′(x)=3x2-3x=3x(x-1),
当f′(x)>0,即3x(x-1)>0时,解得x<0或x>1.
当f′(x)<0,即3x(x-1)<0时,0<x<1.
因此,f(x)的单调递增区间为(-∞,0),(1,+∞);单调递减区间为(0,1).
(2)令f′(x)=0,得x1=0,x2=1
当x在(0,2)上变化时,f′(x),f(x)的变化情况如下表:
∴当x=1时,f(x)有极小值f(1)=
,
又f(0)=8,f(2)=10,
因此,f(x)在区间[0,2]上的最大值是10;最小值是
.
当f′(x)>0,即3x(x-1)>0时,解得x<0或x>1.
当f′(x)<0,即3x(x-1)<0时,0<x<1.
因此,f(x)的单调递增区间为(-∞,0),(1,+∞);单调递减区间为(0,1).
(2)令f′(x)=0,得x1=0,x2=1
当x在(0,2)上变化时,f′(x),f(x)的变化情况如下表:
| x | (0,1) | 1 | (1,2) | ||
| f'(x) | - | 0 | + | ||
| f(x) | 单调递减 |
|
单调递增 |
| 15 |
| 2 |
又f(0)=8,f(2)=10,
因此,f(x)在区间[0,2]上的最大值是10;最小值是
| 15 |
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某种玫瑰花,进货商当天以每支1元从鲜花批发商店购进,以每支2元售出.若当天卖不完,剩余的玫瑰花批发商店以每支0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:支)的频率分布直方图(如图所示),将频率视为概率.
某种玫瑰花,进货商当天以每支1元从鲜花批发商店购进,以每支2元售出.若当天卖不完,剩余的玫瑰花批发商店以每支0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:支)的频率分布直方图(如图所示),将频率视为概率.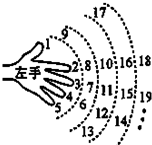 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2014时,对应的指头是
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2014时,对应的指头是