题目内容
直三棱柱ABC—A1B1C1中,∠ACB=120°,AC=CB=A1A=1.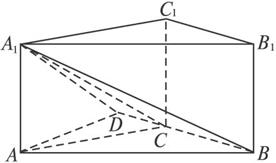
(1)求证:B1C1∥平面A1BC;
(2)求三棱锥A—A1CB的体积;
(3)求二面角A1-CB-A的正切值.
解法一:(1)证明:在三棱柱中C1B1∥CB,BC平面A1BC,且B1C1![]() 平面A1BC,
平面A1BC,
则B1C1∥平面A1BC.
(2)因为![]() =
=![]() =
=![]() ×1×(
×1×(![]() ×1×1×sin120°)=
×1×1×sin120°)=![]() .
.
(3)在平面ABC内过点A向BC作垂线AD,交BC延长线于点D,连结A1D.

因为A1A⊥平面ABC,所以A1D⊥BD.
所以∠A1DA是二面角A1-CB-A的平面角.容易求出AD=![]() ,
,
所以tan∠A1DA=![]() ,
,
即二面角A1-CB-A的正切值是![]() .
.
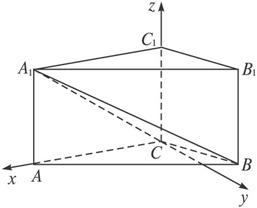
解法二:如图建立空间直角坐标系,则有A(1,0,0),A1(1,0,1),B(![]() ,
,![]() ,0),B1(
,0),B1(![]() ,
,![]() ,1),C1(0,0,1).
,1),C1(0,0,1).
(1)略.
(2)略.
(3)显然n1=(0,0,1)是平面ABC的一个法向量.
设n2=(x,y,z)是平面A1BC的法向量,则n2·![]() =0,且n2·
=0,且n2·![]() =0,即x+z=0,且
=0,即x+z=0,且![]() x+
x+![]() y=0.
y=0.
解得平面A1BC的一个法向量是n2=(1,![]() ,-1).
,-1).
因为n1·n2=-1,|n1|=1,|n2|=![]() ,设二面角A1-CB-A的大小为β,则cos(π-β)=
,设二面角A1-CB-A的大小为β,则cos(π-β)=![]() .所以cosβ=
.所以cosβ=![]() .所以tanβ=
.所以tanβ=![]() .
.

练习册系列答案
相关题目
 直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1=
直三棱柱ABC-A1B1C1中,AC=BC=BB1=1,AB1= 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角. 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( ) 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是







