题目内容
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD= ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.

(1)证明:DE∥平面PBC;
(2)证明:DE⊥平面PAB.
【答案】
(1)参考解析;(2)参考解析.
【解析】
试题分析:(1)直线与平面的平行有两种方法证明第一是在平面内找一条直线与该平面平行,就如本题的证明.E点是中点所以找到PB的中点即可.另外也可以通过平面与平面平行来证明.(2)直线与平面的垂直是要证明该直线与平面内两条相交直线垂直.DE垂直于PA较好证.另外一条又要通过直线AB垂直平面PAD来证明即可.这类题型主要思路是线线关系,线面关系,面面关系之间相互转化.
试题解析:(1)设PB的中点为F,连结EF、CF,EF∥AB,DC∥AB,所以EF∥DC,且EF=DC= .
.
故四边形CDEF为平行四边形,可得ED∥CF.
又ED 平面PBC,CF
平面PBC,CF 平面PBC,
平面PBC,
故DE∥平面PBC.
(2)因为PD⊥底面ABCD,AB 平面ABCD,所以AB⊥PD.
平面ABCD,所以AB⊥PD.
又因为AB⊥AD,PD AD=D,AD
AD=D,AD 平面PAD,PD
平面PAD,PD 平面PAD,所以AB⊥平面PAD.
平面PAD,所以AB⊥平面PAD.
ED 平面PAD,故ED⊥AB.又PD=AD,E为PA的中点,故ED⊥PA;
平面PAD,故ED⊥AB.又PD=AD,E为PA的中点,故ED⊥PA;
PA AB=A,PA
AB=A,PA 平面PAB,AB
平面PAB,AB 平面PAB,所以ED⊥平面PAB.
平面PAB,所以ED⊥平面PAB.
考点:1.线面平行.2.线面垂直.


练习册系列答案
相关题目
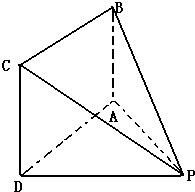 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,且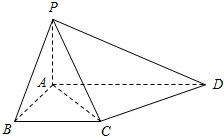 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=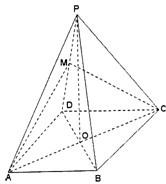 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥CD,AD=BC=2,对角线AC⊥BD于O,∠DAO=60°,且PO⊥平面ABCD,直线PA与底面ABCD所成的角为60°,M为PD上的一点. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.