题目内容
(本题满分14分)已知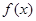 为定义在
为定义在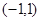 上的奇函数,当
上的奇函数,当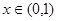 时,
时,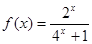 ;
;
(1)求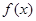 在
在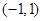 上的解析式;
上的解析式;
(2)试判断函数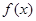 在区间
在区间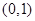 上的单调性,并给出证明.
上的单调性,并给出证明.
【答案】
(1)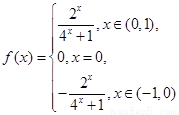 (2)函数
(2)函数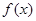 在区间
在区间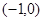 上为单调减函数,证明见解析
上为单调减函数,证明见解析
【解析】
试题分析:(1)当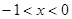 时,
时,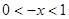 ,
,
所以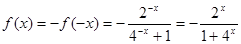 ,
,
又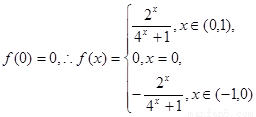 ……6分
……6分
(2)函数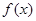 在区间
在区间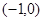 上为单调减函数.
上为单调减函数.
证明:设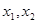 是区间
是区间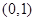 上的任意两个实数,且
上的任意两个实数,且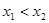 ,
,
则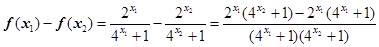
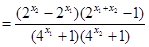 ,
,
因为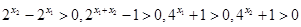 ,
,
所以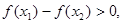 即
即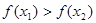 .
.
所以函数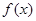 在区间
在区间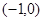 上为单调减函数. ……14分
上为单调减函数. ……14分
考点:本小题主要考查利用奇偶性求分段函数的解析式以及利用定义判定函数的单调性,考查了学生的转化能力和推理能力.
点评:此题第一问求解析式时,不要忘记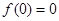 ,证明函数的单调性,只能用单调性的定义或导数(选修中将会学到).
,证明函数的单调性,只能用单调性的定义或导数(选修中将会学到).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
