题目内容
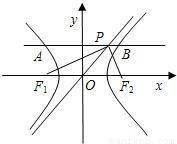
如图,双曲线C的渐近线是2x±3y=0,且两顶点间的距离为6,求该双曲线的方程.分析:分焦点在 x轴上和焦点在 y轴上2种情况,分别根据渐近线方程、2顶点间的距离求出实半轴、虚半轴的长,写出标准方程.
解答:解:当焦点在x轴上时,∵双曲线C1的渐近线是2x±3y=0,∴
=
,
∵两顶点间的距离为6,∴a=3,b=2,
∴双曲线的方程是
-
=1.
当焦点在y轴上时,∵双曲线C1的渐近线是2x±3y=0,∴
=
.
∵两顶点间的距离为6,∴a=3,b=
,
双曲线的方程是
-
=1.
综上,双曲线的方程为:
-
=1,或
-
=1.
| b |
| a |
| 2 |
| 3 |
∵两顶点间的距离为6,∴a=3,b=2,
∴双曲线的方程是
| x2 |
| 9 |
| y2 |
| 4 |
当焦点在y轴上时,∵双曲线C1的渐近线是2x±3y=0,∴
| a |
| b |
| 2 |
| 3 |
∵两顶点间的距离为6,∴a=3,b=
| 9 |
| 2 |
双曲线的方程是
| y2 |
| 9 |
| 4x2 |
| 81 |
综上,双曲线的方程为:
| x2 |
| 9 |
| y2 |
| 4 |
| y2 |
| 9 |
| 4x2 |
| 81 |
点评:本题考查双曲线的标准方程和性质的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
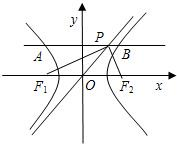 我们定义双曲线C:
我们定义双曲线C: ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,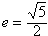 。
。
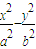 =1(a>0,b>0)的渐近线与直线y=±b的交点为“虚近点”,如图点P是双曲线C在第一象限的渐近点,直线y=b与双曲线C的左、右分支分别交于点A、B,F1、F2分别是双曲线C的左、右焦点,O为坐标原点.
=1(a>0,b>0)的渐近线与直线y=±b的交点为“虚近点”,如图点P是双曲线C在第一象限的渐近点,直线y=b与双曲线C的左、右分支分别交于点A、B,F1、F2分别是双曲线C的左、右焦点,O为坐标原点.