题目内容
2．8人排成两排，每排4人，下列各有多少种不同的排法？（1）甲、乙在前排两端，丙在后排左端；
（2）甲、乙在前排，丙在后排．
分析 （1）先排前排，除甲乙丙外选2人排在甲乙之间，再排后排，丙在后排左端，把剩下的3人全排列，根据分步计数原理可得．
（2）先排前排，除甲乙丙外选2人和甲乙全排列，再排后排，丙和剩下的3人全排列，根据分步计数原理可得．
解答 解：（1）先排前排，除甲乙丙外选2人排在甲乙之间，再排后排，丙在后排左端，把剩下的3人全排列，故有${A}_{2}^{2}•{A}_{5}^{2}•{A}_{3}^{3}$=240种；
（2）先排前排，除甲乙丙外选2人和甲乙全排列，再排后排，丙和剩下的3人全排列，故有${C}_{5}^{2}•{A}_{4}^{4}$$•{A}_{4}^{4}$=5760种；
点评 本题考查了分步计数原理，充分体现了元素分析法（优先考虑特殊元素）、位置分析法（优先考虑特殊位置）．
练习册系列答案
相关题目
12．一个几何体的三视图如图所示，其中俯视图与左视图均为半径是2的圆，则这个几何体的体积是（ ）
| A． | 14π | B． | 12π | C． | 8π | D． | 16π |
17．
某几何体的三视图如图所示，则该几何体的表面积为（ ）
某几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | 16 | B． | （10+$\sqrt{5}$）π | C． | 4+（5+$\sqrt{5}）π$π | D． | 6+（5+$\sqrt{5}）$π |
7．已知正数等比数列{an}，a1=1，a3=2，则a1a2+a3a4+a5a6+…+a2n-1a2n的值为（ ）
| A． | $\sqrt{2}$（2n-1） | B． | 2（2n-1） | C． | $\frac{\sqrt{2}（{4}^{n}-1）}{3}$ | D． | $\frac{2（{4}^{n}-1）}{3}$ |
11．
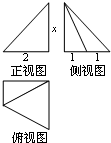某几何体的三视图如图所示，且该几何体的体积是6，则正视图中的x的值是（ ）
某几何体的三视图如图所示，且该几何体的体积是6，则正视图中的x的值是（ ）| A． | 9 | B． | 8 | C． | 3 | D． | 6 |
