题目内容
在平面直角坐标系xOy中，过坐标原点的一条直线与函数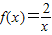
的图象交于P、Q两点，则线段PQ长的最小值是 ．
【答案】分析：由题意和函数的图象关于原点对称知当过原点的直线的斜率是1时，直线与函数图形的交点之间的距离最短，写出直线的方程，求出直线与函数的交点坐标，利用两点之间的距离公式得到结果．
解答：解：由题意知当过原点的直线的斜率是1时，直线与函数图形的交点之间的距离最短，
而y=x与y=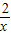
的两个交点的坐标是（
，
）（-
，-
），
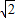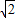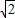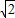∴根据两点之间的距离公式得到|PQ|=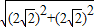
=
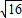=4，
故答案为：4
点评：本题考查反比例函数的图形的特点，考查直线与双曲线之间的交点坐标的求法，考查两点之间的距离公式，是一个综合题目．
解答：解：由题意知当过原点的直线的斜率是1时，直线与函数图形的交点之间的距离最短，
而y=x与y=
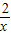的两个交点的坐标是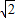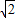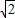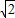（，）（-，-），∴根据两点之间的距离公式得到|PQ|=
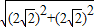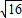==4，故答案为：4
点评：本题考查反比例函数的图形的特点，考查直线与双曲线之间的交点坐标的求法，考查两点之间的距离公式，是一个综合题目．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是