题目内容
已知函数 的图象与x轴相切于点S(s,0).
的图象与x轴相切于点S(s,0).(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数f(x)的图象与过坐标原点O的直线l相切于点T(t,f(t)),且f(t)≠0,证明:1<t<e;(注:e是自然对数的底)
【答案】分析:(Ⅰ)求导函数,利用函数 的图象与x轴相切于点S(s,0),建立方程,可求函数的解析式;
的图象与x轴相切于点S(s,0),建立方程,可求函数的解析式;
(Ⅱ)由切线过点T(t,f(t))得到关于实数t的方程 ,将问题转化为函数
,将问题转化为函数 的零点区间判定问题,排除零点在区间
的零点区间判定问题,排除零点在区间 内是该题的一个难点(在(Ⅰ)的启发下,想到
内是该题的一个难点(在(Ⅰ)的启发下,想到 是区间
是区间 内的唯一零点,但因
内的唯一零点,但因 而排除).
而排除).
解答:(Ⅰ)解:由 ,得
,得 .…(1分)
.…(1分)
∵函数 的图象与x轴相切于点S(s,0),
的图象与x轴相切于点S(s,0),
∴ ,…①且f(s)=
,…①且f(s)= ….②…(2分)
….②…(2分)
联立①②得c=e, .…(3分)
.…(3分)
∴ .…(4分)
.…(4分)
(Ⅱ)证明:求导函数得 .
.
∵函数 的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
∴直线l的方程为: ,
,
又∵T在直线l上,∴实数t必为方程 ….③的解.…(5分)
….③的解.…(5分)
令 ,则
,则 ,
,
解g′(t)>0得 ,g′(t)<0得
,g′(t)<0得 .
.
∴函数y=g(t)在 递减,在
递减,在 递增.…(7分)
递增.…(7分)
∵ ,且函数y=g(t)在
,且函数y=g(t)在 递减,
递减,
∴ 是方程
是方程 在区间
在区间 内的唯一一个解,
内的唯一一个解,
又∵ ,∴
,∴ 不合题意,即
不合题意,即 .…(8分)
.…(8分)
∵g(1)=2-e<0, ,函数y=g(t)在
,函数y=g(t)在 递增,
递增,
∴必有1<t<e.…(10分)
点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、曲线的切线方程、函数的零点、解不等式、直线方程和三角函数等基础知识,考查运算求解能力、推理论证能力、抽象概括能力,考查数形结合思想、化归与转化思想、函数与方程思想、特殊与一般思想.
 的图象与x轴相切于点S(s,0),建立方程,可求函数的解析式;
的图象与x轴相切于点S(s,0),建立方程,可求函数的解析式;(Ⅱ)由切线过点T(t,f(t))得到关于实数t的方程
 ,将问题转化为函数
,将问题转化为函数 的零点区间判定问题,排除零点在区间
的零点区间判定问题,排除零点在区间 内是该题的一个难点(在(Ⅰ)的启发下,想到
内是该题的一个难点(在(Ⅰ)的启发下,想到 是区间
是区间 内的唯一零点,但因
内的唯一零点,但因 而排除).
而排除).解答:(Ⅰ)解:由
 ,得
,得 .…(1分)
.…(1分)∵函数
 的图象与x轴相切于点S(s,0),
的图象与x轴相切于点S(s,0),∴
 ,…①且f(s)=
,…①且f(s)= ….②…(2分)
….②…(2分)联立①②得c=e,
 .…(3分)
.…(3分)∴
 .…(4分)
.…(4分)(Ⅱ)证明:求导函数得
 .
.∵函数
 的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,∴直线l的方程为:
 ,
,又∵T在直线l上,∴实数t必为方程
 ….③的解.…(5分)
….③的解.…(5分)令
 ,则
,则 ,
,解g′(t)>0得
 ,g′(t)<0得
,g′(t)<0得 .
.∴函数y=g(t)在
 递减,在
递减,在 递增.…(7分)
递增.…(7分)∵
 ,且函数y=g(t)在
,且函数y=g(t)在 递减,
递减,∴
 是方程
是方程 在区间
在区间 内的唯一一个解,
内的唯一一个解,又∵
 ,∴
,∴ 不合题意,即
不合题意,即 .…(8分)
.…(8分)∵g(1)=2-e<0,
 ,函数y=g(t)在
,函数y=g(t)在 递增,
递增,∴必有1<t<e.…(10分)
点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、曲线的切线方程、函数的零点、解不等式、直线方程和三角函数等基础知识,考查运算求解能力、推理论证能力、抽象概括能力,考查数形结合思想、化归与转化思想、函数与方程思想、特殊与一般思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
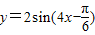
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )


 的图象与x轴交点为
的图象与x轴交点为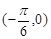 ,相邻最高点坐标为
,相邻最高点坐标为 .
.  的表达式;
的表达式; 的单调增区间;
的单调增区间; 在
在 上的最值.
上的最值. 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 B.
B.
 D.
D.
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 B.
B.
 D.
D.