Question

函数是定义在区间(2k-1，2k+1)(k∈Z)上的奇函数，且对任意x∈(2k-1，2k+1)(k∈Z)均有f(x+2)=f(x)成立，当x∈[0，1)时，f(x)=a^1-x-a，(0＜a＜1)

(1)求f(x)的表达式；

(2)解不等式f(x)＞-a．

Answer 1

解：(1)∵f(x)是奇函数，

∴当x∈(-1，1)时，f(-x)=-f(x)

设x∈(-1，0)，则-x∈(0，1)，

而x∈(0，1)时，f(x)=a^1-x-a，

∴f(-x)=a^1+x-a=-f(x)

∴f(x)=a-a^1+x．

∴f（x）=.

又f（x+2）=f(x)，

∴f(x)为周期函数，且周期T=2．

∴f(x)=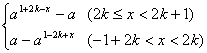(k∈Z)

(2)当0≤x＜1时，

f(x)＞-aa^1-x-a＞-a

a^1-x＞．而0＜a＜1．∴＜x＜1．

当-1＜x＜0时，由于a-a^1+x＜0．-a＞0

因而不可能有f(x)＞-a．

∴f(x)＞-a在(-1，1)上的解为：＜x＜1．

由函数的周期性可知：+2k＜x＜2k+1．(A∈Z).