Question

在直三棱柱A₁B₁C₁—ABC中，BC=CC₁，当底面△A₁B₁C₁满足条件_______时，有AB₁⊥BC₁.(注：填上你认为正确的一种条件即可，不必考虑所有可能的情况)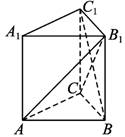

Answer 1

解析：连结B₁C，由BC=CC₁，可得BC₁⊥B₁C，

    因此，要证AB₁⊥BC₁，则只要证BC₁⊥平面AB₁C，

    即只要证AC⊥BC₁即可.

    由直三棱柱可知，只要证AC⊥BC.

    因A₁C₁∥AC，B₁C₁∥BC，故只要A₁C₁⊥B₁C₁即可(或者能推导出A₁C₁⊥B₁C₁的条件，如∠A₁C₁B₁=90°等).

答案：A₁C₁⊥B₁C₁