题目内容
已知函数f（x）在定义域（0，+∞）上是单调函数．若对任意x∈（0，+∞）都有f(f(x)-
)=4，则f（4）=
| 4 | x |
3
3
．分析：令t=f(x)-
，则f(x)=t+
，由已知中对任意x∈（0，+∞）都有f(f(x)-
)=4，我们可构造方程求出t值，进而代入x=4可得答案．
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
解答：解：令t=f(x)-
，则f(x)=t+
∵对任意x∈（0，+∞）都有f(f(x)-
)=4，
∴f（t）=4=t+
，
解得t=2
∴f(4)=2+
=3
故答案为：3
| 4 |
| x |
| 4 |
| x |
∵对任意x∈（0，+∞）都有f(f(x)-
| 4 |
| x |
∴f（t）=4=t+
| 4 |
| t |
解得t=2
∴f(4)=2+
| 4 |
| 4 |
故答案为：3
点评：本题考查的知识点是函数的值，函数解析式的求法，其中抽象函数解析式的求法，要注意对已知条件及未知条件的凑配思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
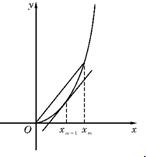已知函数f（x）=x3+x2，数列|xn|（xn＞0）的第一项xn=1，以后各项按如下方式取定：曲线x=f（x）在（xn+1，f（xn+1））处的切线与经过（0，0）和（xn，f （xn））两点的直线平行（如图）．
中ξi的选取是任意的，且In仅于n有关．