题目内容
 (考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在二题中任选一题作答,如果多做,则按所做的第一题评分)(1)(几何证明选做题)如图,已知RT△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则
| BD |
| DA |
| 16 |
| 9 |
| 16 |
| 9 |
(2)(坐标系与参数方程选做题)已知圆C的圆心是直线
|
(x+1)2+y2=2
(x+1)2+y2=2
.分析:(1)先计算AB,再利用切割线定理,从而可求得结论;
(2)利用参数方程确定圆心坐标,利用圆心到直线的距离,确定半径,从而可得圆的方程.
(2)利用参数方程确定圆心坐标,利用圆心到直线的距离,确定半径,从而可得圆的方程.
解答:解:(1)∵RT△ABC的两条直角边AC,BC的长分别为3cm,4cm,
∴AB=5,又由切割线定理得BC2=BD•AB,∴BD=
、
于是,DA=AB-BD=5-
=
、
故所求
=
×
=
、
(2)令y=0得t=-1,所以直线
(t为参数)与x轴的交点为(-1,0),因为直线与圆相切,所以圆心到直线的距离等于半径,即r=
=
,故圆C的方程为(x+1)2+y2=2.
故答案为:
,(x+1)2+y2=2
∴AB=5,又由切割线定理得BC2=BD•AB,∴BD=
| 16 |
| 5 |
于是,DA=AB-BD=5-
| 16 |
| 5 |
| 9 |
| 5 |
故所求
| BD |
| DA |
| 16 |
| 5 |
| 5 |
| 9 |
| 16 |
| 9 |
(2)令y=0得t=-1,所以直线
|
| |-1+0+3| | ||
|
| 2 |
故答案为:
| 16 |
| 9 |
点评:本题主要考查平面几何中的直线与圆的综合,考查直线的参数方程、圆的方程、直线与圆的位置关系等基础知识,要注意有关定理的灵活运用、

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 的实数解集为_________
的实数解集为_________  的底边
的底边 以
以 点为极点,
点为极点, 为极轴,则顶点
为极轴,则顶点 的极坐标方程为________________.
的极坐标方程为________________. = .
= . (t为参数)与x轴的交点,且圆C与直线x+y+3=0相切.则圆C的方程为 .
(t为参数)与x轴的交点,且圆C与直线x+y+3=0相切.则圆C的方程为 .
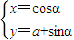 (α为参数)与曲线ρ2-2ρcosθ=0的交点个数为 个.
(α为参数)与曲线ρ2-2ρcosθ=0的交点个数为 个.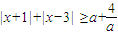 对任意的实数x恒成立,则实数a的取值范围是 .
对任意的实数x恒成立,则实数a的取值范围是 .