题目内容
已知{an}是一个公差大于0的等差数列,且满足a3a5=45,a2+a6=14.
(I)求{an}的通项公式;
(Ⅱ)若数列{bn}满足: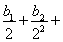 …
…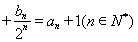 ,求{bn}的前n项和.
,求{bn}的前n项和.
【答案】
(I)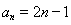 ;(Ⅱ)
;(Ⅱ)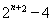
【解析】
试题分析:(I)由已知条件解方程组可得首项和公差,通项公式即可求出。(Ⅱ)利用整体思想根据题意可知数列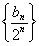 的前
的前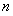 项和为
项和为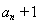 。由数列前
。由数列前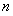 项和可求数列
项和可求数列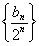 通项公式
通项公式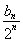 ,即可求得数列{bn}的通项公式及前前n项和。
,即可求得数列{bn}的通项公式及前前n项和。
试题解析:解:(Ⅰ)设等差数列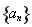 的公差为
的公差为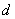 ,则依题设
,则依题设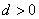 .
.
由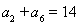 ,可得
,可得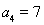 .
.
由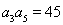 ,得
,得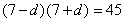 ,可得
,可得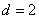 .
.
所以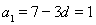 .
.
可得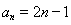 . 6分
. 6分
(Ⅱ)设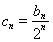 ,则
,则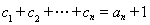 .
.
即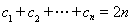 ,
,
可得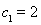 ,且
,且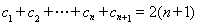 .
.
所以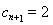 ,可知
,可知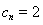
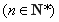 .
.
所以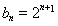 ,
,
所以数列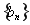 是首项为
是首项为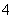 ,公比为
,公比为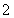 的等比数列.
的等比数列.
所以前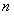 项和
项和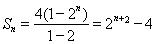 . 13分
. 13分
考点:等差数列通项公式、用数列前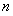 项和求数列通项公式。
项和求数列通项公式。

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目