题目内容
已知数列{an}满足对任意的n∈N*,都有an>0,且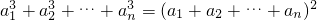 .
.
(1)求a1,a2的值;
(2)求数列{an}的通项公式an;
(3)求数列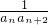 的前n项和为Sn.
的前n项和为Sn.
(1)解:当n=1时,有 ,由于an>0,所以a1=1.
,由于an>0,所以a1=1.
当n=2时,有 ,将a1=1.代入上式,由于an>0,,所以a2=2.
,将a1=1.代入上式,由于an>0,,所以a2=2.
(2)解:由于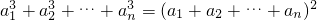 ,①
,①
则有 =
= . ②
. ②
②-①,得

由于an>0,所以 ③
③
同样有 n≥2,④
n≥2,④
③-④,得 . 所以an+1-an=1.
. 所以an+1-an=1.
由于a2-a1=1,即当n≥1时都有an+1-an=1.
所以数列{an}是首项为1,公差为1的等差数列.故an=n.
(3)解:由(2)知an=n, =
= .
.
所以 (1-
(1-
 )
)
=


=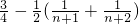 .
.
分析:(1)令n=1,2可以求a1=1,a2=2.
(2)由已知可得 =
= ,两式相减,结合an>0可求得
,两式相减,结合an>0可求得 ,则可得
,则可得 ,n≥2,两式相减整理可得an+1-an=1,从而可得数列{an}是等差数列,可求
,n≥2,两式相减整理可得an+1-an=1,从而可得数列{an}是等差数列,可求
(3)由(2)知 =
= ,利用裂项可求和
,利用裂项可求和
点评:本题主要考查了利用数列的递推公式求解数列的项,及构造等差数列求解通项公式,还考查了裂项求解数列的和,要注意 =
= 中的系数
中的系数 不要漏掉
不要漏掉
 ,由于an>0,所以a1=1.
,由于an>0,所以a1=1.当n=2时,有
 ,将a1=1.代入上式,由于an>0,,所以a2=2.
,将a1=1.代入上式,由于an>0,,所以a2=2.(2)解:由于
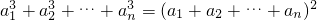 ,①
,①则有
 =
= . ②
. ②②-①,得


由于an>0,所以
 ③
③同样有
 n≥2,④
n≥2,④③-④,得
 . 所以an+1-an=1.
. 所以an+1-an=1.由于a2-a1=1,即当n≥1时都有an+1-an=1.
所以数列{an}是首项为1,公差为1的等差数列.故an=n.
(3)解:由(2)知an=n,
 =
= .
.所以
 (1-
(1-
 )
)=



=
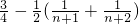 .
.分析:(1)令n=1,2可以求a1=1,a2=2.
(2)由已知可得
 =
= ,两式相减,结合an>0可求得
,两式相减,结合an>0可求得 ,则可得
,则可得 ,n≥2,两式相减整理可得an+1-an=1,从而可得数列{an}是等差数列,可求
,n≥2,两式相减整理可得an+1-an=1,从而可得数列{an}是等差数列,可求(3)由(2)知
 =
= ,利用裂项可求和
,利用裂项可求和点评:本题主要考查了利用数列的递推公式求解数列的项,及构造等差数列求解通项公式,还考查了裂项求解数列的和,要注意
 =
= 中的系数
中的系数 不要漏掉
不要漏掉 
练习册系列答案
相关题目