题目内容
a、b、c分别是△ABC内角∠A,∠B,∠C的对边,若△ABC的周长为 ,且
,且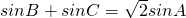 ,则边长a的值为
,则边长a的值为
- A.

- B.2
- C.4
- D.

C
分析:根据正弦定理把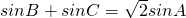 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
解答:根据正弦定理,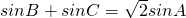 可化为
可化为
∵△ABC的周长为 ,
,
∴联立方程组 ,
,
解得a=4.
∴边长a=4;
故选C.
点评:本题的考点是正弦定理,主要考查正弦定理的运用,将角转化为边是关键.
分析:根据正弦定理把
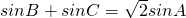 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.解答:根据正弦定理,
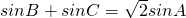 可化为
可化为
∵△ABC的周长为
 ,
,∴联立方程组
 ,
,解得a=4.
∴边长a=4;
故选C.
点评:本题的考点是正弦定理,主要考查正弦定理的运用,将角转化为边是关键.

练习册系列答案
相关题目
在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,则∠A=( )
| A、30° | B、60° | C、120° | D、150° |



