题目内容
已知函数f(x)=log2(ax2-x+ )在[1,
)在[1, ]上恒正,则实数a的取值范围是________.
]上恒正,则实数a的取值范围是________.
a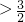
分析:根据对数函数的性质求解.函数f(x)=log2(ax2-x+ )在[1,
)在[1, ]上恒正等价于ax2-x+
]上恒正等价于ax2-x+ >1的解集一定包含
>1的解集一定包含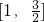 .
.
解答:∵函数f(x)=log2(ax2-x+ )在[1,
)在[1, ]上恒正,
]上恒正,
依据对数函数的单调性,
∴ax2-x+ >1即2ax2-2x-1>0的解集一定包含
>1即2ax2-2x-1>0的解集一定包含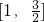 ,
,
∴ ,
,
∴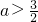 .
.
点评:求解对数函数问题时,解题过程中要考虑对数函数的定义域.
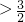
分析:根据对数函数的性质求解.函数f(x)=log2(ax2-x+
 )在[1,
)在[1, ]上恒正等价于ax2-x+
]上恒正等价于ax2-x+ >1的解集一定包含
>1的解集一定包含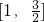 .
.解答:∵函数f(x)=log2(ax2-x+
 )在[1,
)在[1, ]上恒正,
]上恒正,依据对数函数的单调性,
∴ax2-x+
 >1即2ax2-2x-1>0的解集一定包含
>1即2ax2-2x-1>0的解集一定包含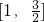 ,
,∴
 ,
,∴
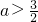 .
.点评:求解对数函数问题时,解题过程中要考虑对数函数的定义域.

练习册系列答案
相关题目