题目内容
若 表示
表示 的区间长度,函数
的区间长度,函数
 的值域区间长度为
的值域区间长度为 ,则实数
,则实数 的值是( )
的值是( )
| A.4 | B.2 | C. | D.1 |
A
解析本题考查函数最值的求法。解决根式的函数和方程,平方是常用的方法。由题意分析知,可先确定函数的最值,再求解 。
。
平方, 。则令
。则令 。解出其最值即得答案。
。解出其最值即得答案。
由二次函数的性质知, 的最大值和最小值分别为
的最大值和最小值分别为 和
和 。
。
故 的最大值和最小值分别为
的最大值和最小值分别为 。
。
所以 的值域区间长度为
的值域区间长度为 。故选 A.
。故选 A.
这要求学生能够分析问题,化繁为简。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若函数 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( )
| A.2 | B. | C. | D. |
奇函数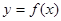 在区间[3,7]上是增函数,且最小值为-5,那么
在区间[3,7]上是增函数,且最小值为-5,那么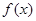 在区间[-7,-3]
在区间[-7,-3]
| A.是增函数且最小值为5 | B.是增函数且最大值为5 |
| C.是减函数且最小值为5 | D.是减函数且最大值为5 |
下列结论正确的是 ( )
A.当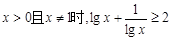 | B.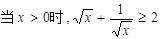 |
C.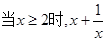 的最小值为2 的最小值为2 | D.当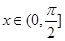 时, 时, 的最小值是4 的最小值是4 |
如果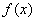 是定义在
是定义在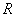 的增函数,且
的增函数,且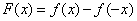 ,那么
,那么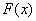 一定是
一定是
A.奇函数,且在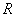 上是增函数 上是增函数 | B.奇函数,且在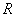 上是减函数 上是减函数 |
C.偶函数,且在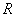 上是增函数 上是增函数 | D.偶函数,且在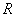 上是减函数 上是减函数 |
函数 的反函数为 ( )
的反函数为 ( )
A. | B. |
C. | D. |
已知函数f(x)= 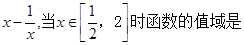 ( )
( )
A.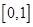 | B.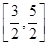 | C.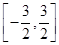 | D.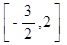 |
 为正三角形,四边形ABCD为正方形,平面
为正三角形,四边形ABCD为正方形,平面 .点M为平面ABCD内的一个动点,且满足
.点M为平面ABCD内的一个动点,且满足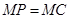 .则点M在正方形ABCD内的轨迹为
.则点M在正方形ABCD内的轨迹为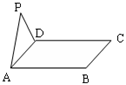
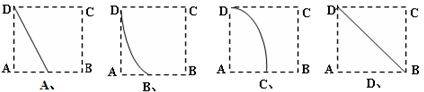
 的大致图象是
的大致图象是