Question

已知函数f(x)=sin(2x-

π

6

)
（Ⅰ）求函数y=f（x）的单调增区间；      
（Ⅱ）求函数f（x）在区间[-

π

12

，

π

2

]上的值域；
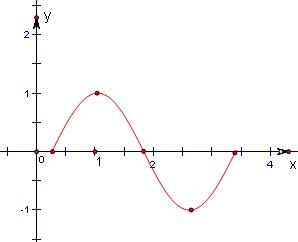
（Ⅲ）画出函数y=f（x）在一个周期上的简图．

Answer 1

分析：（I）利用y=sinx的单调性，求出函数的单调增区间．
（II）利用正弦函数的图象与性质，即可求出函数f（x）在区间[-

π

12

，

π

2

]上的值域．
（III）利用描点法画函数图象，第一步列表，令函数解析式中的角分别为0，

π

2

，π，

3π

2

，2π，求出x的值，且代入函数解析式求出对应的函数值y的值，找出函数图象上五点坐标，在平面直角坐标系中描出五个点，用平滑的曲线画出函数图象即可；

解答：解：（I）令u=2x-

π

6

，则函数y=3sinu的单调增区间为[-

π

2

+2kπ，

π

2

+2kπ]k∈Z（5分）
由-

π

2

+2kπ≤2x-

π

6

≤

π

2

+2kπ，得：
-

π

6

+kπ≤x≤

π

3

+kπk∈Z
函数y=3sin（2x-

π

6

）的单调增区间为：[-

π

6

+kπ，

π

3

+kπ]k∈Z（8分）
（II）∵x∈[-

π

12

，

π

2

]，可得2x-

π

6

∈[-

π

3

，

5π

6

]
∴当2x-

π

6

=

π

2

，即x=

π

3

时，函数的取最大值为1
又∵f（-

π

12

）=-

3

2

＜f（

π

2

）=

1

2

，
∴当x=

π

12

时，函数取最小值-

3

2

，
综上所述，函数f（x）在区间[-

π

12

，

π

2

]上的值域为[-

3

2

，1]．
（III）根据题意列出表格得：

t	0	π 2	π	3π 2	2π
x	π 12	π 3	7π 12	5π 6	13π 12
y	0	1	0	-1	0

简图：

点评：本题考查五点法作函数y=Asin（ωx+φ）的图象，正弦函数的单调性，考查计算能力，是基础题．