题目内容
 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=
- A.

- B.

- C.
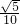
- D.

B
分析:法一:由题意,可得∠CED=∠AED-∠AEC,根据图象可得tan∠AED=1,tan∠AEC= ,从而有tan∠CED=tan(∠AED-∠AEC)=
,从而有tan∠CED=tan(∠AED-∠AEC)= =
= =
= ,再由三角函数的定义即可求出sin∠CED选出正确选项
,再由三角函数的定义即可求出sin∠CED选出正确选项
法二:用余弦定理在三角形CED中直接求角的余弦,再由同角三角关系求正弦;
法三:在三角形CED中用正弦定理直接求正弦
解答:由题设及图知∠CED=∠AED-∠AEC,
又正方形ABCD的边长为1,延长BA至E,使AE=1
∴tan∠AED=1,tan∠AEC=
∴tan∠CED=tan(∠AED-∠AEC)= =
= =
=
由图知,可依EC所在直线为X轴,以垂直于EC的线向上的方向为Y轴建立坐标系,又∠CED锐角,由三角函数的定义知,∠CED终边一点的坐标为(3,1),此点到原点的距离是

故sin∠CED= =
=
故选B
法二:利用余弦定理
在△CED中,根据图形可求得ED= ,CE=
,CE= ,
,
由余弦定理得cos∠CED= ,
,
∴sin∠CED= =
=
故选B
法三:在△CED中,根据图形可求得ED= ,CE=
,CE= ,∠CDE=135°
,∠CDE=135°
由正弦定理得 ,即
,即
故选B
点评:本题考查任意角三角函数的定义及两角各与差的正切函数,解题的关键是根据图象求出tan∠CED,本题综合考查了正切的差角公式及三角函数的定义,综合性强,知识性强,题后要注意总结做题的规律
分析:法一:由题意,可得∠CED=∠AED-∠AEC,根据图象可得tan∠AED=1,tan∠AEC=
 ,从而有tan∠CED=tan(∠AED-∠AEC)=
,从而有tan∠CED=tan(∠AED-∠AEC)= =
= =
= ,再由三角函数的定义即可求出sin∠CED选出正确选项
,再由三角函数的定义即可求出sin∠CED选出正确选项法二:用余弦定理在三角形CED中直接求角的余弦,再由同角三角关系求正弦;
法三:在三角形CED中用正弦定理直接求正弦
解答:由题设及图知∠CED=∠AED-∠AEC,
又正方形ABCD的边长为1,延长BA至E,使AE=1
∴tan∠AED=1,tan∠AEC=

∴tan∠CED=tan(∠AED-∠AEC)=
 =
= =
=
由图知,可依EC所在直线为X轴,以垂直于EC的线向上的方向为Y轴建立坐标系,又∠CED锐角,由三角函数的定义知,∠CED终边一点的坐标为(3,1),此点到原点的距离是


故sin∠CED=
 =
=
故选B
法二:利用余弦定理
在△CED中,根据图形可求得ED=
 ,CE=
,CE= ,
,由余弦定理得cos∠CED=
 ,
,∴sin∠CED=
 =
=
故选B
法三:在△CED中,根据图形可求得ED=
 ,CE=
,CE= ,∠CDE=135°
,∠CDE=135°由正弦定理得
 ,即
,即
故选B
点评:本题考查任意角三角函数的定义及两角各与差的正切函数,解题的关键是根据图象求出tan∠CED,本题综合考查了正切的差角公式及三角函数的定义,综合性强,知识性强,题后要注意总结做题的规律

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为