题目内容
设f(x)是定义在R上的奇函数,且当x≥0 时,f(x)=x2.若对任意的x∈[t,t+1],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是
- A.[
 ,+∞)
,+∞) - B.[
 ,+∞)
,+∞) - C.(0,
 ]
] - D.(-∞,-
 ]u[
]u[ ,+∞)
,+∞)
A
分析:由f(x)是定义在R上的奇函数,且当x≥0 时,f(x)=x2可求得当x<0时的解析式,又x∈[t,t+1],分t+1≤0与t≥0两种情况讨论,从而将不等式f(x+t)≥2f(x)恒成立,转化为关于变量x的二次不等式在x∈[t,t+1]上的恒成立问题来解决.
解答:∵f(x)是定义在R上的奇函数,且当x≥0 时,f(x)=x2
∴当x<0,有-x>0,f(-x)=(-x)2,
∴-f(x)=x2,即f(x)=-x2,
∴f(x)=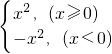 ;
;
又对任意的x∈[t,t+1],不等式f(x+t)≥2f(x)恒成立,
∴当t+1<0,即t<-1,2t≤x+t≤2t+1<-1,此时有:-(x+t)2≥-2x2①恒成立,x∈[t,t+1].
①变形为:x2-2tx-t2≥0恒成立,x∈[t,t+1].
令g(x)=x2-2tx-t2,其对称轴x=t,g(x)在[t,t+1]单调递增,g(x)min=g(t)=-2t2<0,故t<-1,不满足题意;
当t>0,0<2t≤x+t≤2t+1,由任意的x∈[t,t+1],不等式f(x+t)≥2f(x)恒成立,可得:(x+t)2≥2x2②,x∈[t,t+1];
②变形为:x2-2tx-t2≤0恒成立,x∈[t,t+1];令g(x)=x2-2tx-t2,其对称轴x=t,g(x)在[t,t+1]单调递增,要使x2-2tx-t2≤0恒成立,x∈[t,t+1];只需
g(x)max=g(t+1)=(t+1)2-2t(t+1)-t2≤0,即1-2t2≤0,
解得:t≥ .
.
综上所述:t≥ .
.
故选A.
点评:本题考查函数奇偶性的性质,难点在于得到函数解析式后的分类讨论,着重考查学生利用函数的性质解决恒成立问题,属于难题.
分析:由f(x)是定义在R上的奇函数,且当x≥0 时,f(x)=x2可求得当x<0时的解析式,又x∈[t,t+1],分t+1≤0与t≥0两种情况讨论,从而将不等式f(x+t)≥2f(x)恒成立,转化为关于变量x的二次不等式在x∈[t,t+1]上的恒成立问题来解决.
解答:∵f(x)是定义在R上的奇函数,且当x≥0 时,f(x)=x2
∴当x<0,有-x>0,f(-x)=(-x)2,
∴-f(x)=x2,即f(x)=-x2,
∴f(x)=
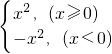 ;
;又对任意的x∈[t,t+1],不等式f(x+t)≥2f(x)恒成立,
∴当t+1<0,即t<-1,2t≤x+t≤2t+1<-1,此时有:-(x+t)2≥-2x2①恒成立,x∈[t,t+1].
①变形为:x2-2tx-t2≥0恒成立,x∈[t,t+1].
令g(x)=x2-2tx-t2,其对称轴x=t,g(x)在[t,t+1]单调递增,g(x)min=g(t)=-2t2<0,故t<-1,不满足题意;
当t>0,0<2t≤x+t≤2t+1,由任意的x∈[t,t+1],不等式f(x+t)≥2f(x)恒成立,可得:(x+t)2≥2x2②,x∈[t,t+1];
②变形为:x2-2tx-t2≤0恒成立,x∈[t,t+1];令g(x)=x2-2tx-t2,其对称轴x=t,g(x)在[t,t+1]单调递增,要使x2-2tx-t2≤0恒成立,x∈[t,t+1];只需
g(x)max=g(t+1)=(t+1)2-2t(t+1)-t2≤0,即1-2t2≤0,
解得:t≥
 .
.综上所述:t≥
 .
.故选A.
点评:本题考查函数奇偶性的性质,难点在于得到函数解析式后的分类讨论,着重考查学生利用函数的性质解决恒成立问题,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |