题目内容
若a>0,b>0,函数y=
解:依题意,得![]() [a2x+2(ab)x-b2x+1]<0.
[a2x+2(ab)x-b2x+1]<0.
∴a2x+2(ab)x-b2x+1>1,即a2x+2(ab)x-b2x>0.
左式是关于ax、bx的二次“齐次”式.
两边同除以b2x,得(![]() )2x+2(
)2x+2(![]() )x-1>0.
)x-1>0.
∴(![]() )x>
)x>![]() -1或(
-1或(![]() )x<-1-
)x<-1-![]() (负值舍去).
(负值舍去).
∴当a>b,即![]() >1时,x>
>1时,x>![]() (
(![]() -1);
-1);
当a=b,即![]() =1时,x∈R;
=1时,x∈R;
当a<b,即![]() <1时,x<
<1时,x<![]() (
(![]() -1).
-1).
综上,得解集(略).

练习册系列答案
相关题目




 的定义域为R,若存在与
的定义域为R,若存在与 无关的正常数M,使
无关的正常数M,使 对一切实数
对一切实数 ;
; ;
; ;
; .其中是“有界泛函”的个数为 ( )
.其中是“有界泛函”的个数为 ( ) 的定义域为R,若存在与
的定义域为R,若存在与 无关的正常数M,使
无关的正常数M,使 对一切实数
对一切实数 ;
; ;
; ;
;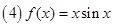 .其中是“有界泛函”的个数为 ( )
.其中是“有界泛函”的个数为 ( ) )的定义域为R,若存在与
)的定义域为R,若存在与 对一切实数
对一切实数 ②f(
②f( ④
④ 其中是“有界泛函”的个数为(
)
其中是“有界泛函”的个数为(
)