题目内容
【题目】已知函数![]() (
(![]() )在定义域内仅有唯一零点.
)在定义域内仅有唯一零点.
(1)若对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(2)设函数![]() ,对于
,对于![]() ,
, ![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)直接求导即可得到函数的增减性,只有一个零点,说明其极值为零,即可得到答案;
(2)通过对不等式的变形化简,得到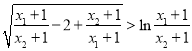 的形式,此时自然运用换元法得到一个新的不等式
的形式,此时自然运用换元法得到一个新的不等式![]() ,再利用导数来对其进行证明即可。
,再利用导数来对其进行证明即可。
试题解析:
(1)由![]() (
(![]() ),得
),得![]() .
.
令![]() ,解得
,解得![]() .
.
显然![]() ,即
,即![]() 在
在![]() 的定义域
的定义域![]() 内,
内,
于是当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上递增,在区间
上递增,在区间![]() 上递减,则
上递减,则![]() .
.
因为![]() 在定义域内仅有唯一零点,所以
在定义域内仅有唯一零点,所以![]() ,即
,即![]() ,
,
从而![]() .
.
于是不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
①当![]() 时,取
时,取![]() ,得
,得![]() ,而
,而![]() ,所以
,所以![]() 不恒成立,即
不恒成立,即![]() 不满足条件;
不满足条件;
②当![]() 时,令
时,令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,
, ![]() .
.
(i)若![]() ,即
,即![]() 时,当
时,当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上递增,
上递增,
从而恒有![]() ,即
,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 满足条件.
满足条件.
(ii)若![]() ,即
,即![]() 时,当
时,当![]() ,
, ![]() ,则
,则![]() 递减,
递减,
于是当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 不恒成立,即
不恒成立,即![]() 不满足条件.
不满足条件.
综上得![]() ,即
,即![]() .
.
(2)由![]() ,得
,得![]() ,不妨令
,不妨令![]() ,
,
欲证![]() ,
,
只需证![]() ,
,
即证![]() ,
,
只需证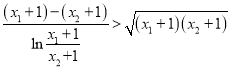 ,
,
只需证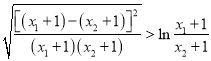 ,
,
即证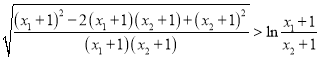 ,
,
即证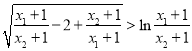 .
.
令![]() (
(![]() ),则只需证
),则只需证![]() ,即
,即![]() .
.
令![]() ,则
,则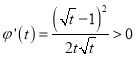 ,
,
于是![]() 在
在![]() 上递增,从而
上递增,从而![]() ,
,
即![]() ,即
,即![]() ,所以原不等式成立.
,所以原不等式成立.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目