题目内容
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿
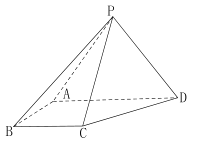
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() 。若该三棱锥的顶点
。若该三棱锥的顶点![]() 在底面
在底面![]() 的射影
的射影![]() 在线段
在线段![]() 上,设
上,设![]() ,则
,则![]() 的取值范围为______.
的取值范围为______.
【答案】![]()
【解析】
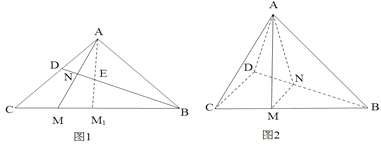
解![]() 可得其为等腰直角三角形,有题意可知折叠前图(1)中
可得其为等腰直角三角形,有题意可知折叠前图(1)中![]() ,根据等腰直角三角形位置关系可推出
,根据等腰直角三角形位置关系可推出![]() ,在(2)图中,
,在(2)图中,![]() 为
为![]() 的斜边,得
的斜边,得![]() ,即可得出答案.
,即可得出答案.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
![]() ,
,
所以![]() 为等腰直角三角形.
为等腰直角三角形.
由将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,
,
且![]() 在底面
在底面![]() 的射影
的射影![]() 在线段
在线段![]() 上,
上,
如图2所示,![]() 平面
平面![]() ,则
,则![]() ,
,
过![]() 做
做![]() ,垂足为
,垂足为![]() ,连
,连![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
在折叠前图1中,由![]() ,
,![]() ,
,
所以![]() 三点共线.取
三点共线.取![]() 中点
中点![]() ,
,
连![]() 交
交![]() 于
于![]() ,由
,由![]() 为等腰直角三角形,
为等腰直角三角形,
所以![]() 在线段
在线段![]() 之间,故
之间,故![]() 为钝角,
为钝角,
![]() ,所以
,所以![]() 在
在![]() 之间,得
之间,得![]() 在
在![]() 之间,
之间,
所以![]() ,即
,即![]() .
.
在图2中,由于![]() 为
为![]() 的斜边,
的斜边,
![]() 为直角边,所以
为直角边,所以![]() ,即
,即![]() .
.
所以![]() .
.
故答案为:![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目