题目内容
已知y=f（x）是定义在R上的偶函数，且f（x）在[0，+∞）上是减函数，实数x1，x2满足x1＜0，x2＞0，x1+x2=2a-1，且有f（x1）＜f（x2），则实数a的取值范围是（ ）A．a＞0
B．a＜0
C．
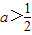
D．
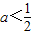
【答案】分析：由自变量离原点越近函数值越大，可得x2离原点较近，由此可得结论．
解答：解：∵f（x）在[0，+∞）上是减函数，y=f（x）是定义在R上的偶函数
∴f（x）在（-∞，0）上是增函数，
∴自变量离原点越近函数值越大，
∵f（x1）＜f（x2），
∴x2离原点较近
∵x1＜0，x2＞0，
∴x1+x2＜0
∵x1+x2=2a-1，
∴2a-1＜0
∴
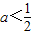
故选D．
点评：本题考查函数奇偶性与单调性的综合，解题的关键是根据题设条件得出函数的变化规律，属于基础题．
解答：解：∵f（x）在[0，+∞）上是减函数，y=f（x）是定义在R上的偶函数
∴f（x）在（-∞，0）上是增函数，
∴自变量离原点越近函数值越大，
∵f（x1）＜f（x2），
∴x2离原点较近
∵x1＜0，x2＞0，
∴x1+x2＜0
∵x1+x2=2a-1，
∴2a-1＜0
∴
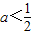
故选D．
点评：本题考查函数奇偶性与单调性的综合，解题的关键是根据题设条件得出函数的变化规律，属于基础题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
已知函数f（x）=x+
已知函数f（x）=2x+